library(tidyverse)
library(sgsur)3 Exploratory data analysis
Every data analysis journey begins the same way: you are faced with a dataset that needs to be understood. Before we try to explain, predict, or test anything, the first and most natural step is simply to look and explore the data. That activity is called exploratory data analysis (EDA). Think of EDA as an informal “getting-to-know-you” conversation with the data. We are not yet fitting statistical models, conducting formal tests, or drawing conclusions; we are just describing and understanding what is there. We skim the numbers, summarise their main features, sketch quick plots, and reflect on what we see. Along the way, we ask questions like: What types of variables do we have? Where are their centres? How are they spread out and shaped? What relationships exist between variables?
3.1 This chapter covers…
Looking before testing. Exploratory data analysis (EDA) as the curious first pass on any dataset.
Opening and inspecting data. Loading data with the tidyverse and using tibbles as the basic structure for analysis.
Running a quick data health check. Using
print(),glimpse(), andskim()to identify variable types, ranges, and missingness.Visualising distributions. Drawing histograms and boxplots to read centre, spread, and shape at a glance.
Summarising with the right numbers. Using mean, median, and mode for centre; range, IQR, SD, and MAD for spread — and knowing when each applies.
Comparing and relating variables. Making conditional plots and scatterplots with smoothers, and quantifying relationships with Pearson or Spearman correlations.
Building lasting EDA habits. Checking codebooks, confirming variable types, noting outliers and missingness, and keeping brief notes for later modelling.
When working with data, it helps to have a shared language for what we mean by things like “variable” or “observation.” Here’s a quick anatomy lesson.
Data
Recorded values about things in the world (people, places, events), usually measured or classified in a consistent way.
Dataset (data set)
A collection of data, often organised as a rectangular table.
Observation / row / case / record
One unit you’re studying. Examples: one person, one country, one school, or one country–year.
Variable / column / field / feature
An attribute measured on each observation. Examples: age, happiness, gdp.
Value The specific entry in a cell where a row and a column meet.
Data frame (R)
R’s rectangular data structure: rows = observations, columns = variables. A tibble is a modern, friendlier data frame that prints nicely and keeps types stable.
Identifier (ID) / key
A column (or set of columns) that uniquely identifies each row (e.g., person_id, or country + year).
Same ideas, different names
Row ≈ observation ≈ case ≈ record
Column ≈ variable ≈ field ≈ feature
Outcome ≈ response ≈ dependent (use only in clear causal/experimental settings; otherwise prefer “outcome/response”)
Predictor ≈ explanatory ≈ independent (use only in clear causal/experimental settings; otherwise prefer “predictor/explanatory”)
Tidy data (rule of thumb)
Each variable is a column, each observation is a row, each cell holds one value.
Keep different kinds of observations in different tables and link them by keys.
As with most chapters in this book, we will use two packages, tidyverse and sgsur, and so the first step is to load them:
The dataset we will use in this chapter is whr2025, which is built into sgsur. It provides data from the World Happiness Report 2025. For each of 139 countries, the principal variables we have are happiness, a measure of average life satisfaction, and gdp, the gross domestic product (GDP) per person in 2021 international dollars. The lgdp is the base 10 logarithm (see Note 3.2) of gdp, and income divides the countries into three equally sized groups on the basis of their gdp value.
A logarithm is essentially the opposite of an exponent. When we write something like \(2^3 = 8\), we are saying “2 raised to the power of 3 equals 8.” The logarithm asks the reverse question: “What power do I need to raise 2 to in order to get 8?” The answer is 3, so we write \(\log_2(8) = 3\). The small number after “log” is called the base; it tells us which number we are repeatedly multiplying. So \(\log_2(8) = 3\) means “2 to what power equals 8? Answer: 3.” Similarly, \(\log_{10}(1000) = 3\) because \(10^3 = 1000\). When we do not write a base, it is usually assumed to be 10 (common logarithm) or \(e\) (natural logarithm, sometimes written as \(\ln\)). The number \(e\) is a special mathematical constant approximately equal to 2.718 that appears often in mathematical formulas, similar to \(\pi \approx 3.1416\).
Logarithms are used throughout statistics because they have special mathematical properties that make calculations easier and more stable. They turn multiplication into addition, prevent numbers from getting too large or small for computers to handle, and naturally arise in many statistical formulas involving probabilities and exponential relationships.
3.2 Looking, glimpsing, skimming
Once we have our dataset in R, the very first thing to do is to simply look at it.
The whr2025 is built into the sgsur package that we have loaded, so all we have to do is type its name:
whr2025# A tibble: 139 × 6
country iso3c happiness gdp lgdp income
<chr> <chr> <dbl> <dbl> <dbl> <ord>
1 Afghanistan AFG 1.72 1992. 3.30 low
2 Albania ALB 5.30 18244. 4.26 medium
3 Algeria DZA 5.36 15159. 4.18 medium
4 Argentina ARG 6.19 27105. 4.43 medium
5 Armenia ARM 5.46 19230. 4.28 medium
6 Australia AUS 7.06 59553. 4.77 high
7 Austria AUT 6.90 65015. 4.81 high
8 Azerbaijan AZE 4.89 21262. 4.33 medium
9 Bahrain BHR 5.96 57213. 4.76 high
10 Bangladesh BGD 3.89 8242. 3.92 low
# ℹ 129 more rowsThis is a simple act, but it is very informative.
We see from the top line that the dataset is a tibble or data frame (see Note 2.2) with 139 rows and 6 columns.
Next we see the column names:
country,iso3c,happiness, …,income. For some or many of these, it is obvious or we can guess what the variables mean. For example, it is obvious on the basis of the name and also by seeing values likeAfghanistan,Albania,Algeria, …,Zimbabwethatcountryrepresents countries. Most R packages, includingsgsur, provide documentation for the packaged datasets, so doing?whr2025opens a complete description of this data in your Help pane that details what each variable means and where the data came from. Unfortunately, however, it will not always be this clear and easy, see Note 3.3.Next we see the R data types of the variables:
<chr>,<chr>,<dbl>, …,<ord>. These somewhat cryptic labels are very important. There are many tags in general, but the most common ones are:<chr>Sequences of characters or text, anything written inside quotation marks, such as"Australia"or"blue".<dbl>Numeric values that can include decimals (or whole numbers written as decimals), e.g.3.14or42.0.<int>Whole numbers (integers), e.g.42or-7.<lgl>Logical values (Boolean values):TRUE,FALSE.<fct>Categorical values stored as named levels with no built-in order (e.g. hair colours"brown","blonde","red").<ord>Categorical values whose levels have a defined order, so comparisons like"low" < "medium" < "high"make sense.<date>Calendar dates printed asYYYY-MM-DD, e.g.2025-07-03.<dttm>Full date-time stamps printed asYYYY-MM-DD HH:MM:SS, e.g.2025-07-07 13:45:02.<time>Durations or time intervals, printed as a number plus units, e.g.3.2 secs.
How R’s data types relate to statistical data types is something we discuss in Section 3.3.
Next we see the top ten rows of the data frame. Even casually looking over the values we see is often very informative. For example, we can guess that the
happinessvariable is probably on a scale from around 1 to around 8 (in fact, it is from 0 to 10), or thatgdprepresents average income per person in dollars (rather than thousands of dollars), or thatincomehas three levelslow<medium<high, and so on. If we want to see more rows, we can use theprintfunction and usento indicate the number of rows. For example, to see 20 rows, do this:print(whr2025, n=20)# A tibble: 139 × 6 country iso3c happiness gdp lgdp income <chr> <chr> <dbl> <dbl> <dbl> <ord> 1 Afghanistan AFG 1.72 1992. 3.30 low 2 Albania ALB 5.30 18244. 4.26 medium 3 Algeria DZA 5.36 15159. 4.18 medium 4 Argentina ARG 6.19 27105. 4.43 medium 5 Armenia ARM 5.46 19230. 4.28 medium 6 Australia AUS 7.06 59553. 4.77 high 7 Austria AUT 6.90 65015. 4.81 high 8 Azerbaijan AZE 4.89 21262. 4.33 medium 9 Bahrain BHR 5.96 57213. 4.76 high 10 Bangladesh BGD 3.89 8242. 3.92 low 11 Belgium BEL 6.89 64186. 4.81 high 12 Benin BEN 4.38 3721. 3.57 low 13 Bolivia BOL 5.78 9844. 3.99 low 14 Bosnia and Herzegovina BIH 5.88 20126. 4.30 medium 15 Botswana BWA 3.38 18846. 4.28 medium 16 Brazil BRA 6.27 19018. 4.28 medium 17 Bulgaria BGR 5.46 33403. 4.52 medium 18 Burkina Faso BFA 4.55 2482. 3.39 low 19 Cambodia KHM 4.34 6691. 3.83 low 20 Cameroon CMR 4.87 4871. 3.69 low # ℹ 119 more rows
Seeing the column names in a data frame is often helpful but seldom enough. A name like country is easy to decode when the entries read “Australia”, “France”, and so on, yet others (score, cond, A_RGENB, V5) can be quite opaque. Is score a percentage, a 1–10 scale, or something else entirely? And a score of what exactly? To answer questions like these, we require a codebook (sometimes called a data dictionary or README) that spells out each variable’s meaning, units, and provenance. In very well maintained datasets, these will be provided, but data you find somewhere on the web may have nothing more than cryptic column labels. In those cases, you can spend hours piecing together definitions, or even find the data unusable because key details are missing. Column names, then, are a starting clue, not a guarantee: always track down or create a proper codebook before moving beyond a cursory look.
Typing the name of your data frame and scanning the printed preview is something you should always do. It takes seconds to do but always tells you important things. The default view, however, shows only as many columns as can fit across your screen. If your dataset has dozens or hundreds of variables, the remaining columns that cannot easily fit on screen are summarised in a single trailing line such as “and 57 more variables”, leaving most of your data hidden from view. When you need a fuller but still compact overview, use glimpse(), which is part of dplyr (and so loaded if you load tidyverse).
glimpse(whr2025)Rows: 139
Columns: 6
$ country <chr> "Afghanistan", "Albania", "Algeria", "Argentina", "Armenia",…
$ iso3c <chr> "AFG", "ALB", "DZA", "ARG", "ARM", "AUS", "AUT", "AZE", "BHR…
$ happiness <dbl> 1.721, 5.304, 5.364, 6.188, 5.455, 7.057, 6.905, 4.893, 5.95…
$ gdp <dbl> 1992.424, 18244.293, 15159.324, 27104.980, 19230.190, 59552.…
$ lgdp <dbl> 3.299382, 4.261127, 4.180680, 4.433049, 4.283984, 4.774903, …
$ income <ord> low, medium, medium, medium, medium, high, high, medium, hig…As you can see, glimpse() rotates the display so columns become rows, listing every variable with its type tag and a sample of values. Because the output is vertical and terse, you can scroll through wide datasets without losing track of what each column contains, all within the same pane of your console or RStudio window.
After you have examined your data frame by typing its name and then using glimpse(), always complete your initial exploration with the skim() function to get some summary statistics and identify potential data quality issues. The skim() function is part of the skimr package, but it is bundled with sgsur so you do not need to load another package.
skim(whr2025)── Data Summary ────────────────────────
Values
Name whr2025
Number of rows 139
Number of columns 6
_______________________
Column type frequency:
character 2
factor 1
numeric 3
________________________
Group variables None
── Variable type: character ────────────────────────────────────────────────────────────────────────────────────────────
skim_variable n_missing complete_rate min max empty n_unique whitespace
1 country 0 1 4 28 0 139 0
2 iso3c 0 1 3 8 0 139 0
── Variable type: factor ───────────────────────────────────────────────────────────────────────────────────────────────
skim_variable n_missing complete_rate ordered n_unique top_counts
1 income 0 1 TRUE 3 low: 47, med: 46, hig: 46
── Variable type: numeric ──────────────────────────────────────────────────────────────────────────────────────────────
skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
1 happiness 0 1 5.55 1.15 1.72 4.81 5.82 6.42 7.74 ▁▂▆▇▅
2 gdp 0 1 27385. 26279. 1456. 6477. 18244. 43428. 132847. ▇▂▂▁▁
3 lgdp 0 1 4.20 0.499 3.16 3.81 4.26 4.64 5.12 ▃▅▇▇▅As you can see, skim() runs a comprehensive diagnostic sweep over every column and prints a well-formatted text report that fits neatly in the console. At the top, you learn how many rows and columns the dataset contains and what types of variables (text, numbers, categories) are present. Then each block provides variable-by-variable details: how many entries are missing, how many distinct values exist, and key summary statistics (we will cover these in detail in Section 3.5).
Even apart from the summary statistics that we will gloss over right now, skim() provides a more complete picture of your data than basic inspection alone. For example, it can reveal problems such as columns filled with missing data (n_missing is the number of missing values; complete_rate is the proportion of non-missing values), and tells you more about each variable, such as that the income variable is an ordered factor with three distinct values (n_unique = 3), and country has 139 distinct values.
3.3 Data types
Before we go further, let us discuss the important concept of data types in statistics. In statistics, the variables we deal with can be of different types, and recognising these differences is essential for choosing the appropriate analysis. There are different classification systems for data types, but the following are the most widely used types.
- Continuous
- A continuous variable is a numeric variable that can, in principle, take on any value within a given range—not just whole numbers. For instance, the daily temperature in a city might normally range from -5°C to 35°C, and within that range it could take on values like 12°C, 18.6°C, or 22.137°C depending on the precision of the measurement. Continuous data can include both positive and negative values, depending on what is being measured. Common examples of continuous variables include weight, height, temperature, and time.
- Categorical
- A categorical variable represents data where there are a finite number of discrete categories that do not have any particular order, that is, one group is not higher or better than another. Examples include marital status, nationality and hair colour. A variable that contains only two response options, e.g., yes/no, is often called a binary or dichotomous variable. A binary variable whose two values are TRUE and FALSE is sometimes known as a logical or Boolean variable.
- Count
- A count variable is a count or tally of the number of times something has happened or taken place. Count data is similar to continuous data in that it is numeric; however, it differs since values can only take on non-negative integers, e.g., 0, 1, 2. Counts start at 0 and can be unbounded, i.e., have no upper limit, or bounded, i.e., have an upper limit. Examples of count data are the number of doctor visits per year a person makes, the number of children someone has, or the number of times the heart beats in a 10-second interval.
- Ordinal
- An ordinal variable is similar to categorical data in that there are a finite number of discrete categories. However, the categories in ordinal data have an order. For example, educational attainment has an order: postgraduate is a higher level of education than undergraduate, which is higher than high school. Another characteristic of ordinal data is that the distance between the categories may not be equal. For example, language ability might be measured as beginner, intermediate and fluent, but it is not immediately clear how close beginner and intermediate speakers are, or how much more of a language a fluent speaker can understand as compared to an intermediate speaker. Ordinal data are used extensively in social science research and are often encountered in the form of agreement scales, i.e., 1 (strongly disagree) to 5 (strongly agree), and hence are often recorded as numbers. Since ordinal data is often represented numerically, this frequently leads to it being erroneously treated and modelled as a continuous measurement.
R’s data types (character, numeric, factor, logical) describe how the computer stores and handles the data, while statistical data types (continuous, ordinal, categorical, count) describe the mathematical and analytical properties of what the data represents.
Here are some mismatches between them:
- Numeric can represent different statistical types: A numeric variable might be continuous (height), count (number of children), ordinal (1 = disagree, 2 = neutral, 3 = agree), binary categorical (0 = no, 1 = yes), etc.
- Characters can be various types: Text like “high”, “medium”, “low” represents ordinal data, while “red”, “blue”, “green” represents categorical data.
- Categorical variables are not always factors: An unordered factor does represent categorical data, but so too can a character variable.
- Logical variables are a type of categorical variable, but have their own R type.
Just because R stores your survey responses as numeric (1, 2, 3, 4, 5) does not mean you should treat them as continuous data and calculate means. The statistical nature of your data should guide your analysis choices, not just the R data type. Always think about what your data actually represents, not just how R is storing it. The statistical type determines which analyses are appropriate, while the R data type determines which functions will work.
3.4 Visualising distributions
As we now know, the whr2025 dataset records each nation’s average life satisfaction score on a 0–10 scale, along with economic indicators such as GDP per person. Before we compare richer and poorer nations in terms of their average happiness, or examine the relationship between a nation’s income and happiness levels, we need a clearer picture of how happiness and income values are distributed across countries. One of the most effective ways of doing this is to plot the data. While there are many visualisation options, two of the most widely used tools for exploring distributions are histograms and boxplots.
With both of these tools, we want to use them to get a sense of the following characteristics of the distribution:
- centre: what is a typical value, or the middle of the distribution, or the point around which the data cluster.
- spread: the degree to which the data deviate from that centre.
- shape: other properties like the asymmetry in the distribution, the balance of mass in the tails versus the centre, or number of peaks the distribution has (modality).
R offers powerful visualisation tools, chief among them the ggplot2 package in the tidyverse. For brand-new users, however, ggplot2’s code can feel like being thrown in at the deep end, even though plotting should be one of the very first skills you acquire. To bridge that gap, the sgsur package provides lightweight wrapper functions — histogram(), tukeyboxplot(), and scatterplot() — that build ggplot2 graphs with a single line of code; the complexity stays under the hood while you get the picture.
For those curious to see how ggplot2 works under the hood, we include a short box with a gentle introduction to its “layered grammar of graphics.”
The idea
A ggplot is built in layers.
You start with the data and aesthetic mappings (aes()), then add one or more geoms (the things you draw), and optionally scales, facets, and themes.
Each + adds a new layer, and later layers are drawn on top of earlier ones.
Core recipe
1. ggplot(data, aes(...)) — choose the dataset and map variables to aesthetics (x, y, colour, fill, size…).
2. + geom_*() — add a geometric layer (points, lines, bars, boxplots, histograms…).
3. Optional: + facet_*() to split into small multiples, + labs() to label, and + theme() to tweak style.
3.4.1 Example 1: A simple histogram
library(ggplot2)
library(sgsur)
ggplot(whr2025, aes(x = happiness)) +
geom_histogram(bins = 20) +
labs(x = "Happiness (0–10)", y = "Number of countries",
title = "Distribution of life satisfaction")What’s happening?
We map happiness to the x-axis in aes().
geom_histogram() draws the bars, and bins = 20 controls granularity.
labs() adds readable axis labels and a title.
3.4.2 Example 2: A layered scatterplot with a smoother
ggplot(whr2025, aes(x = lgdp, y = happiness, colour = income)) +
geom_point(alpha = 0.8) + # layer 1: points
geom_smooth(se = FALSE) + # layer 2: trend line
labs(x = "log10 GDP per person", y = "Happiness",
colour = "Income group",
title = "Happiness and income") +
theme(legend.position = "bottom")Why this works
aes(colour = income) maps colour to the income tier.
geom_point() draws the cloud of dots, and alpha lowers opacity to reduce points plotting on top of each other (known as “overplotting”)
geom_smooth() adds a trend line, and order matters because layers added later are drawn last.
theme() tweaks layout without changing data.
Optional extension Split the histogram by income with faceting.
ggplot(whr2025, aes(happiness)) +
geom_histogram(bins = 15) +
facet_wrap(~ income) +
labs(x = "Happiness", y = "Number of countries",
title = "Happiness by income group")3.4.3 Histograms
To make a histogram of the distribution of happiness, we can use the histogram() command from the sgsur package:
histogram(happiness, data = whr2025)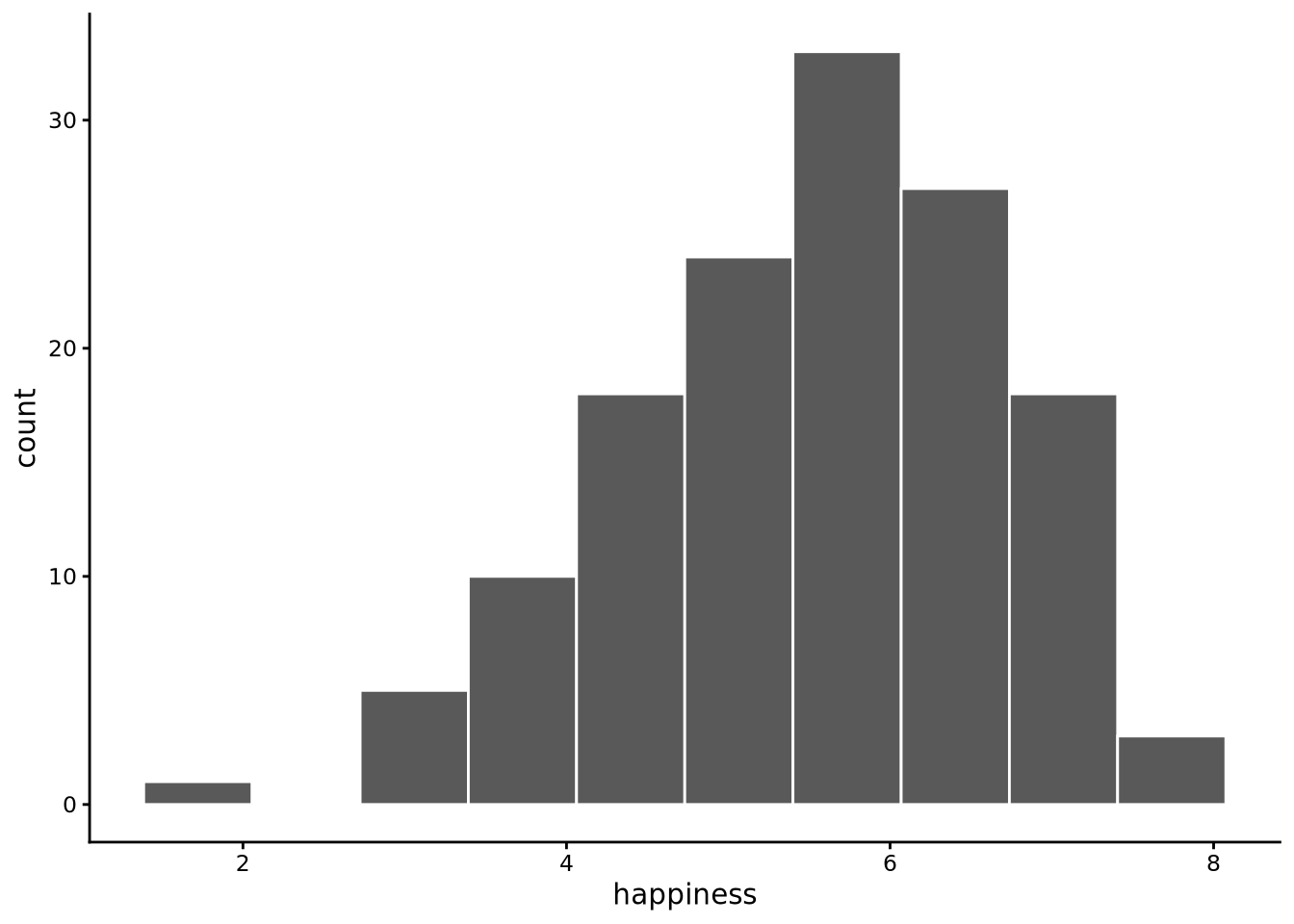
As you can see, all we need to do here is first specify the variable we want to plot, happiness, and then the name of the data frame that contains that variable, whr2025.
A histogram works by dividing the range of your data into intervals (called “bins”) and counting how many data points fall into each interval. By default, histogram() uses 10 bins, but we can change this. Here is how it works step-by-step using happiness from whr2025 with 10 bins:
- Find the data range. Determine the minimum and maximum values in the
happinessvariable. The happiness scores range from 1.72 to 7.74. - Create the bins. Divide this range into 10 equal-width intervals. The total range is 6.02 (7.74 - 1.72), so each bin has a width of 0.602. For example, Bin 1 is from 1.72 to 2.322, Bin 2 is from 2.322 to 2.924, and so on.
- Count the data points. Go through each country’s happiness score and determine which bin it belongs to. A country with a happiness score of 2.8 goes in Bin 2, a score of 5.2 goes in Bin 6, etc.
- Create the visual representation. Draw a bar for each bin where the height represents how many countries fall in that bin and the width represents the bin interval. In principle, the bars are placed adjacent to each other with no gaps. In practice,
ggplot2’s default style shows narrow white lines between bars, and if a bin has zero counts it appears as a gap.
The result is a shape that shows the distribution of happiness scores, revealing patterns like whether most countries cluster around certain values, whether the distribution is symmetric or skewed, and whether there are any outliers.
We can change the number of bins used by the bins argument. By default, bins = 10, but we can set this value to any other positive whole number. The number of bins to use is always a matter of choice; there is no correct answer. If we use too few bins, the histogram may be too coarse and we will miss details:
histogram(happiness, bins = 3, data = whr2025)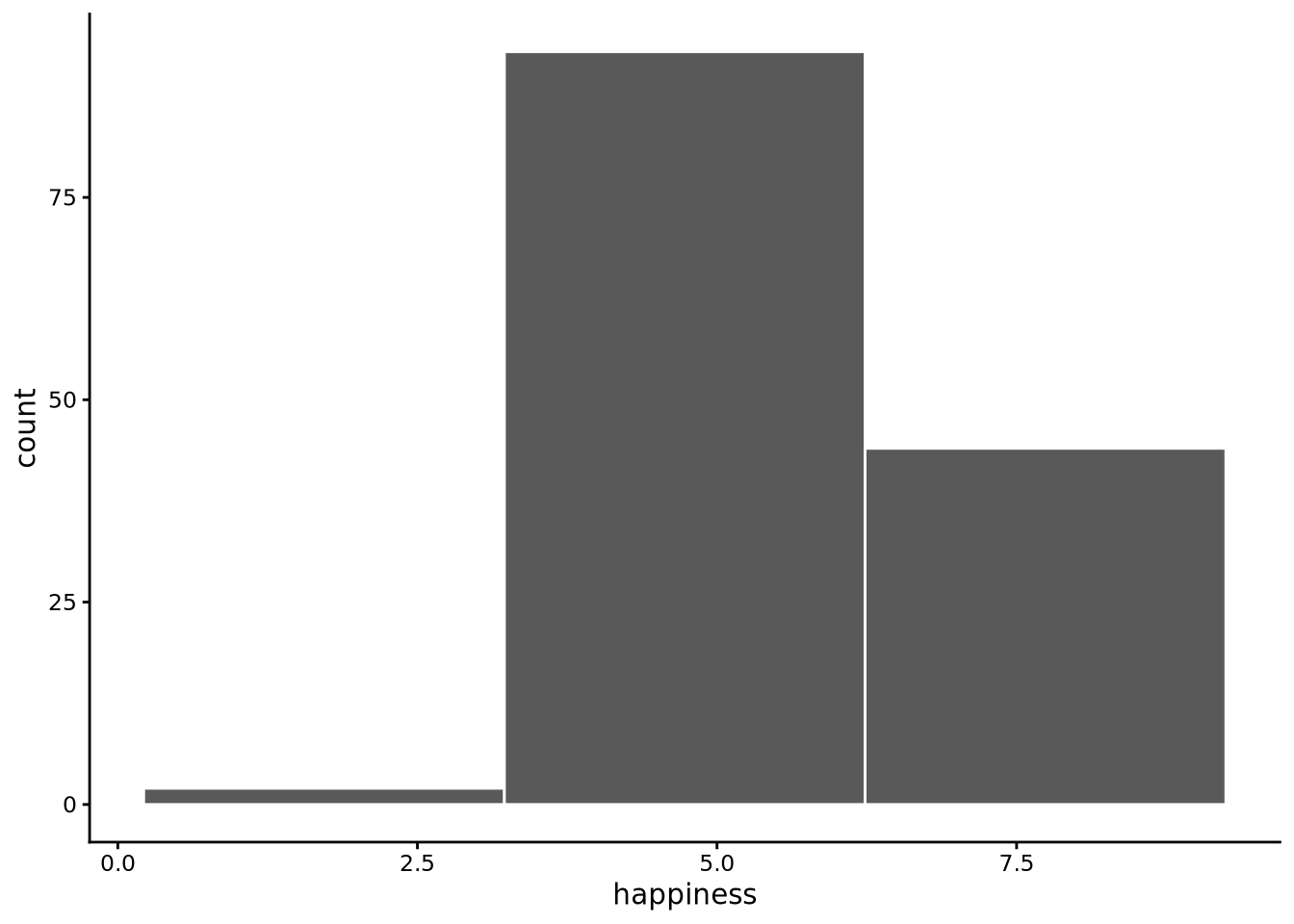
On the other hand, too many bins and the histogram becomes too granular, creating a jagged appearance that obscures the overall pattern:
histogram(happiness, bins = 100, data = whr2025)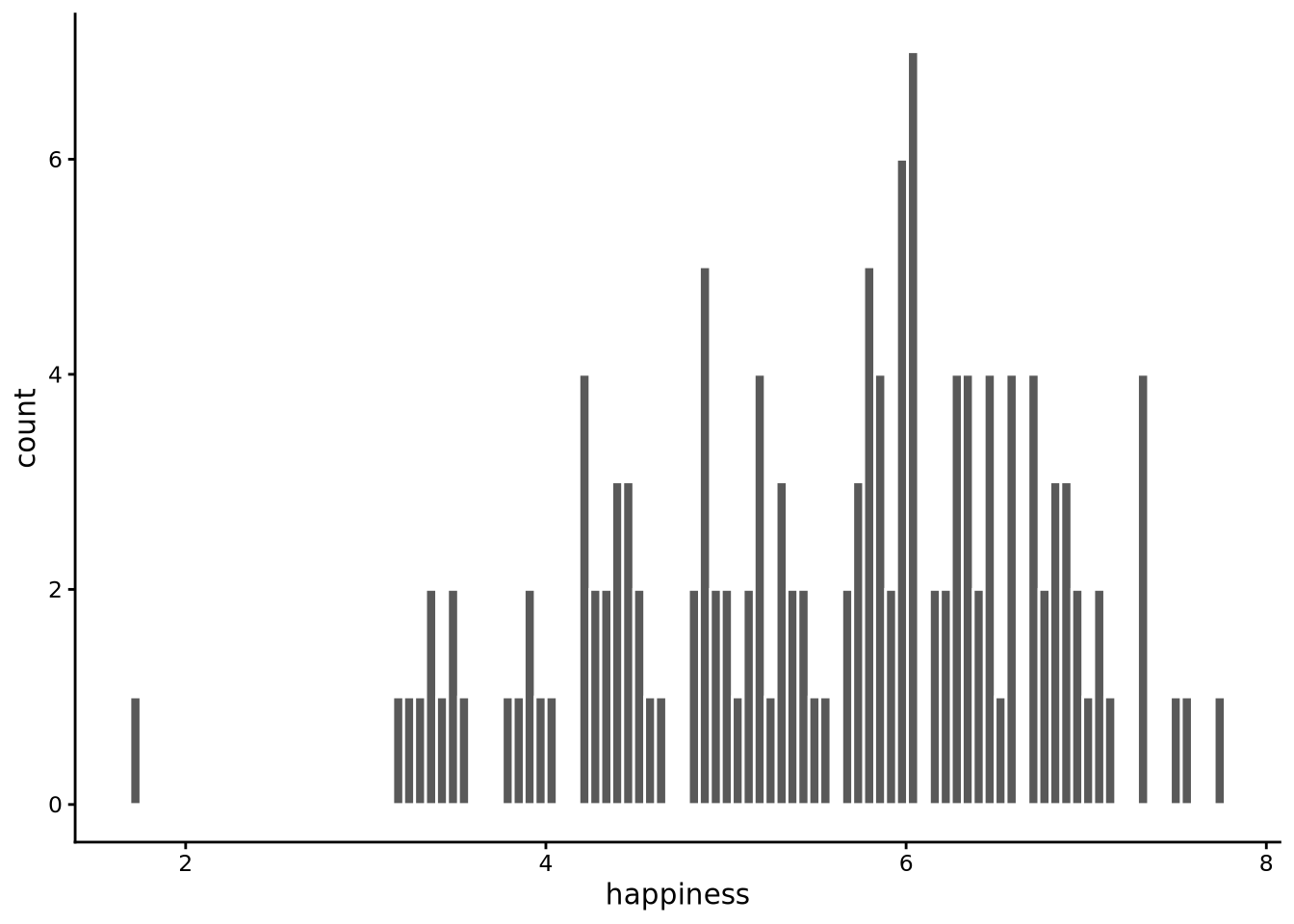
Choosing the right number of bins is ultimately a trade-off between being too coarse (missing important details) and being too noisy (obscuring the overall pattern). The best approach is to experiment with different values and see which one reveals the distribution most clearly. With larger datasets containing thousands or millions of observations, you can typically use many more bins without creating excessive noise, since each bin will still contain enough data points to be meaningful.
In the case of happiness, perhaps around 20 bins is the optimal value: not too coarse, not too noisy:
histogram(happiness, bins=20, data = whr2025)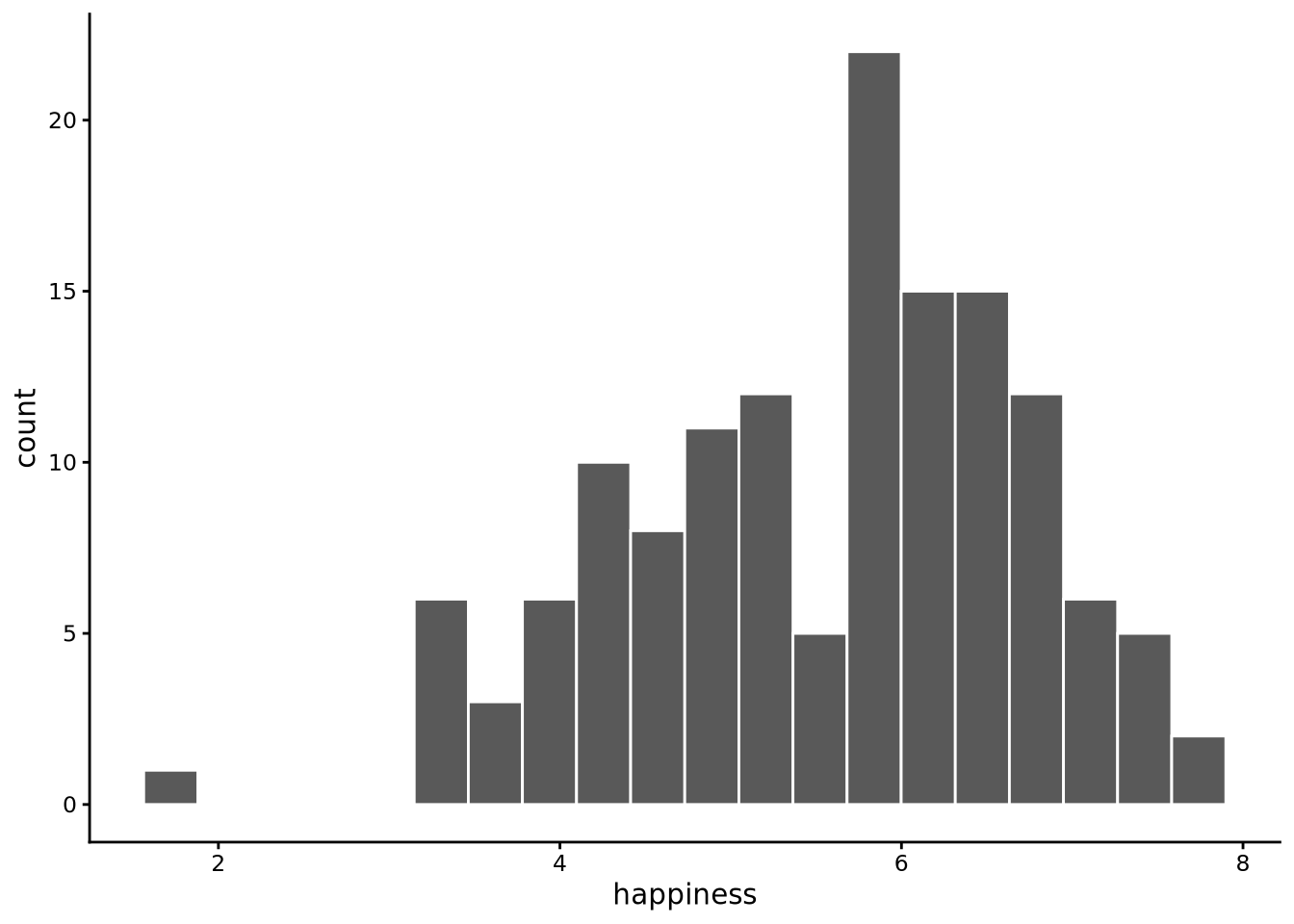
Examining this plot, we can see that the distribution is centred approximately around 6, has one peak, is relatively spread out with values ranging from around 2 to around 8, and is not perfectly symmetrical, with a longer tail to the left, but there are no very extreme values.
The tails of a distribution are the stretched-out ends where the rarer values live. They show how far the data extend away from the main cluster in the centre. A long tail means a few observations lie far from the bulk, while a short tail means almost all values are packed close to the centre. Even when tails are long, they often contain only a thin scattering of observations.
For comparison with happiness, let’s now look at the distribution of the gdp variable.
histogram(gdp, bins=20, data = whr2025)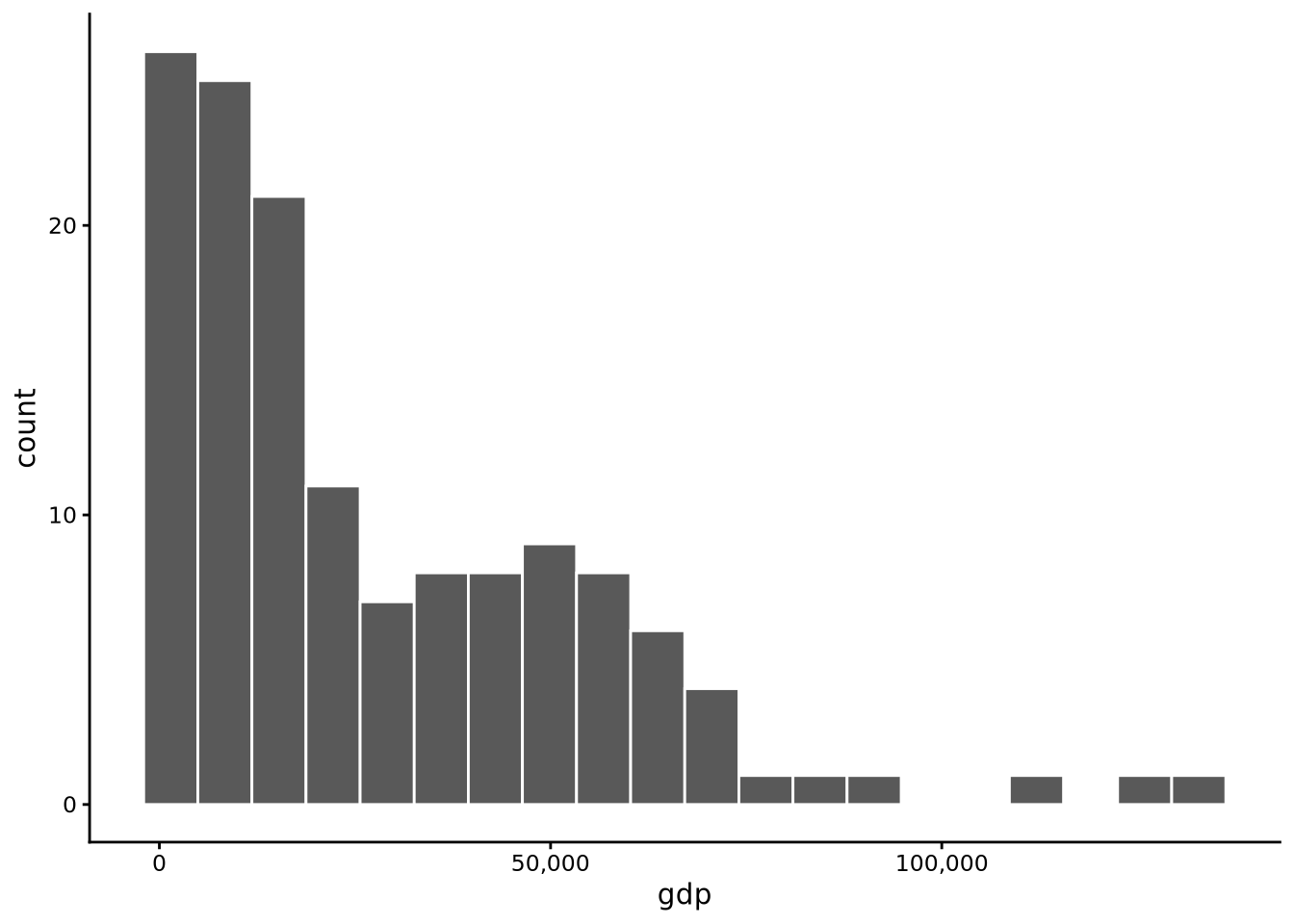
In this case, we see that the distribution is centred somewhere around $25,000 with a relatively long tail to the right. This means that while many countries have relatively low incomes, an increasingly small number have increasingly high incomes. A relatively sizeable minority have incomes at or around $50,000, but the tail stretches as high as to over $100,000.
3.4.4 Boxplots
Boxplots, or more properly called box-and-whisker plots, are an alternative means to plot distributions. There are a few different versions, but the main or standard version is due to the famous statistician John Tukey, and so they are sometimes called Tukey boxplots. In sgsur, the boxplot is implemented with tukeyboxplot().
To visualise the distribution of happiness with a boxplot, use the following command:
tukeyboxplot(happiness, data = whr2025)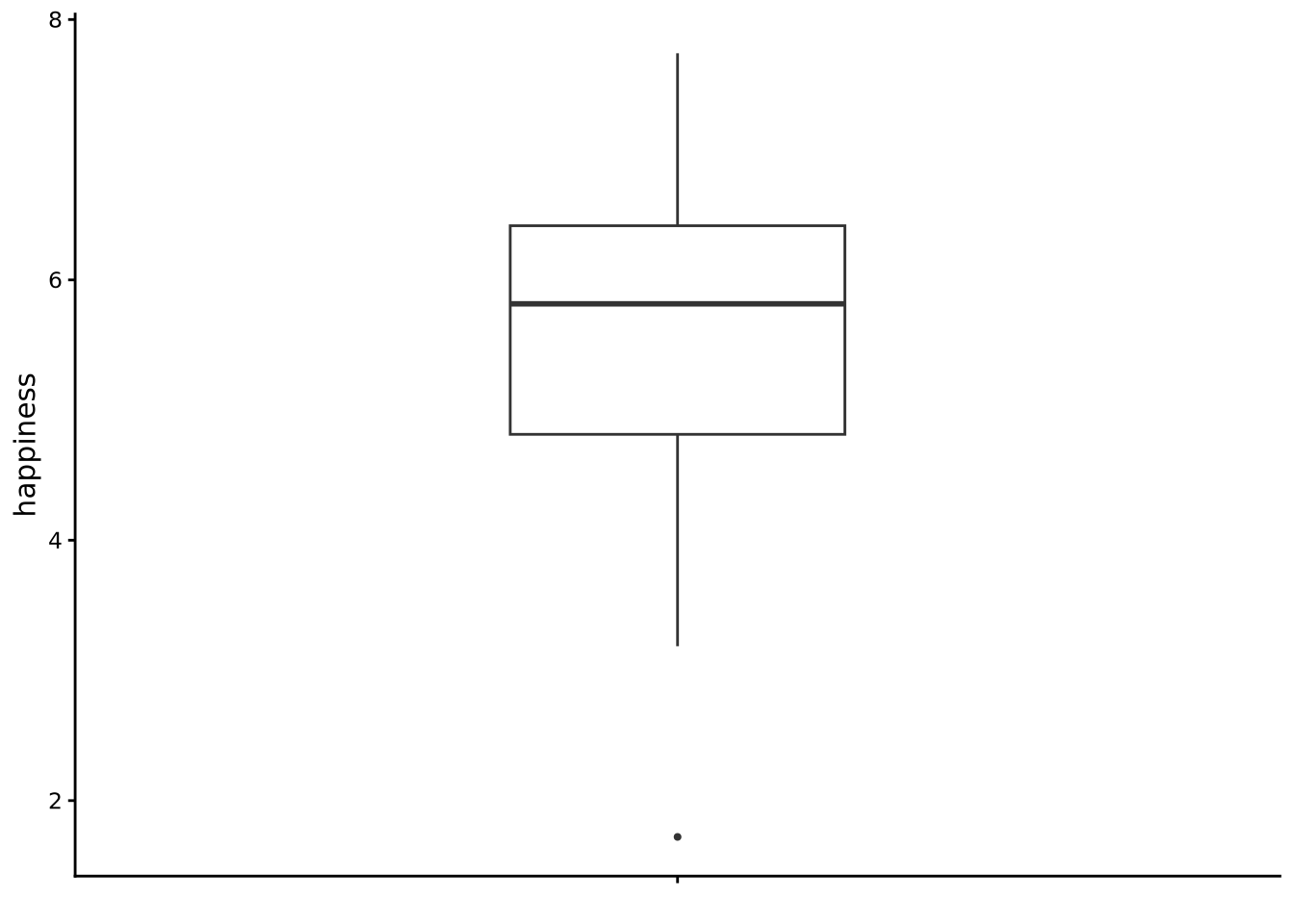
If it makes it easier to visualise, you can flip the axes as follows:
tukeyboxplot(happiness, data = whr2025) + coord_flip()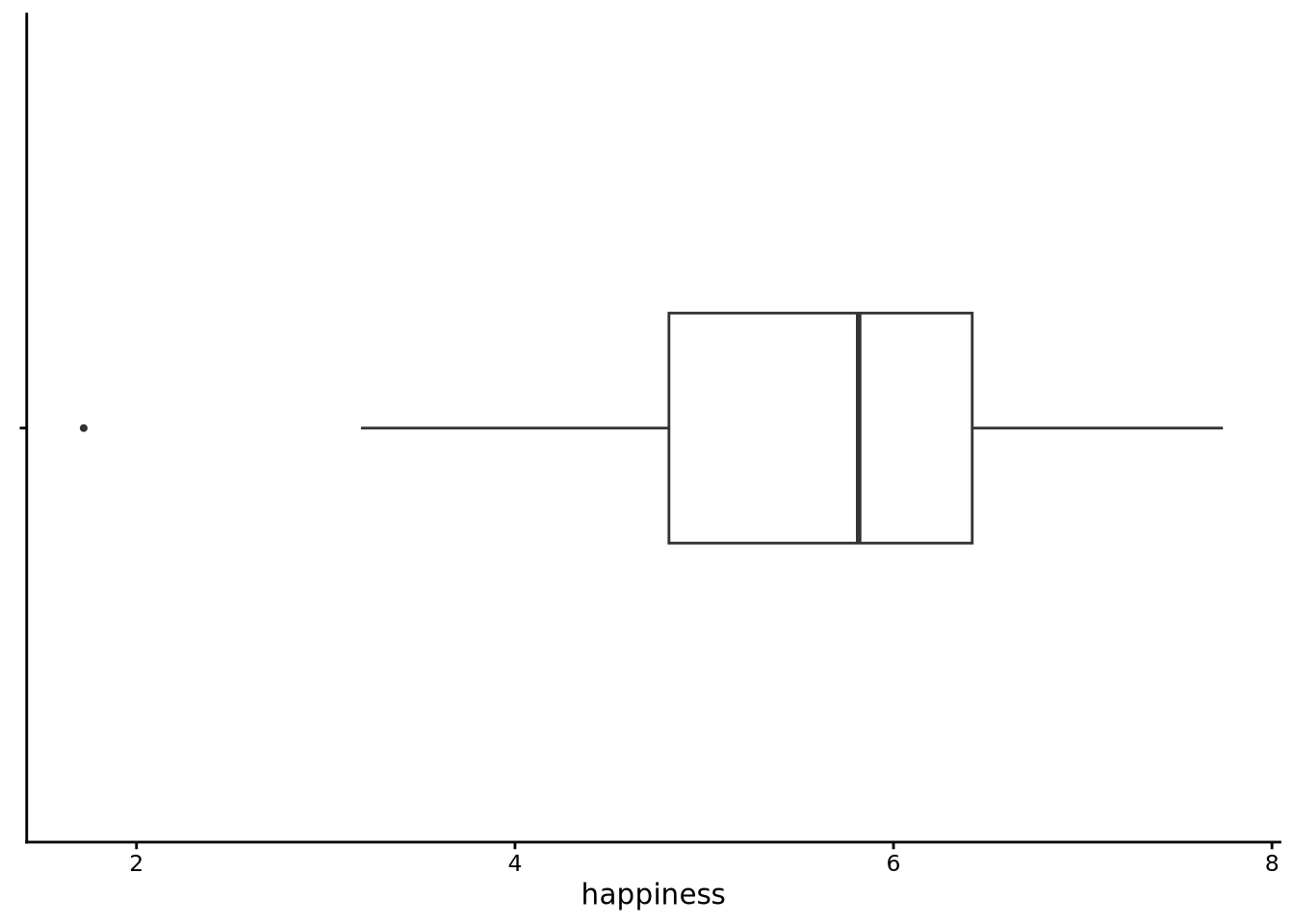
The coord_flip() is from the ggplot2 package, which is part of the tidyverse and so loaded when you load tidyverse or ggplot2 itself, but otherwise will not be.
A Tukey boxplot summarises a distribution with five key numbers and a handful of points. It is calculated as follows:
- Order the data. Sort every value up from smallest to largest.
- Calculate the first, second, and third quartile. We will discuss these in more detail below, but the first quartile (Q1) is the point below which lies 25% of the data (and so 75% of the data is above it). The second quartile (Q2), also known as the median, is the point below which lies 50% of the data (and so 50% is above Q2 too). The third quartile (Q3) is the point above which lies 25% of the data (and so 75% of the data is below it). These Q1, Q2, and Q3 define the box. The lower (or left) edge is Q1, the upper (or right) edge is Q3, and the midline is Q2.
- Measure the IQR. The inter-quartile range (IQR) is the distance from Q1 to Q3. It tells you how wide that middle half is.
- Draw the whiskers. From each end of the box, extend a line out to the most extreme value that is still within 1.5 × IQR of the box edge.
- Flag any outliers. Values beyond the whiskers get their own dots. They are not “errors”; they are simply noticeably higher or lower than most of the data.
Because the boxplot is built on ordered positions (a quarter of the way, halfway, etc.), you can read three things at a glance:
- where the bulk of the values lie (the box),
- how far typical values stray from the centre (the length of the box and whiskers),
- and whether the distribution leans or stretches more on one side (the median not centred in the box; unequal whiskers; many outlier dots on one end).
Looking at the boxplot for happiness, we see the box’s middle bar, signifying Q2 or the median, sits a bit below 6, so we can tell that the typical country reports a life satisfaction score slightly above the mid-scale point (the original scale is from 0 to 10). The box spans roughly 5 to 7, meaning half of all countries fall inside that two-point window while around one quarter of the countries are below 5, and around one quarter are above 7. The lower/left whisker is a bit longer than the right, and a dot appears down near 2: a sign that the lower end stretches out farther than the upper one, which is exactly the left-tail we noticed in the histogram. No dots sit beyond the upper whisker, so extremely high scores are rare.
Let’s now turn to the boxplot for gdp:
tukeyboxplot(gdp, data = whr2025) + coord_flip()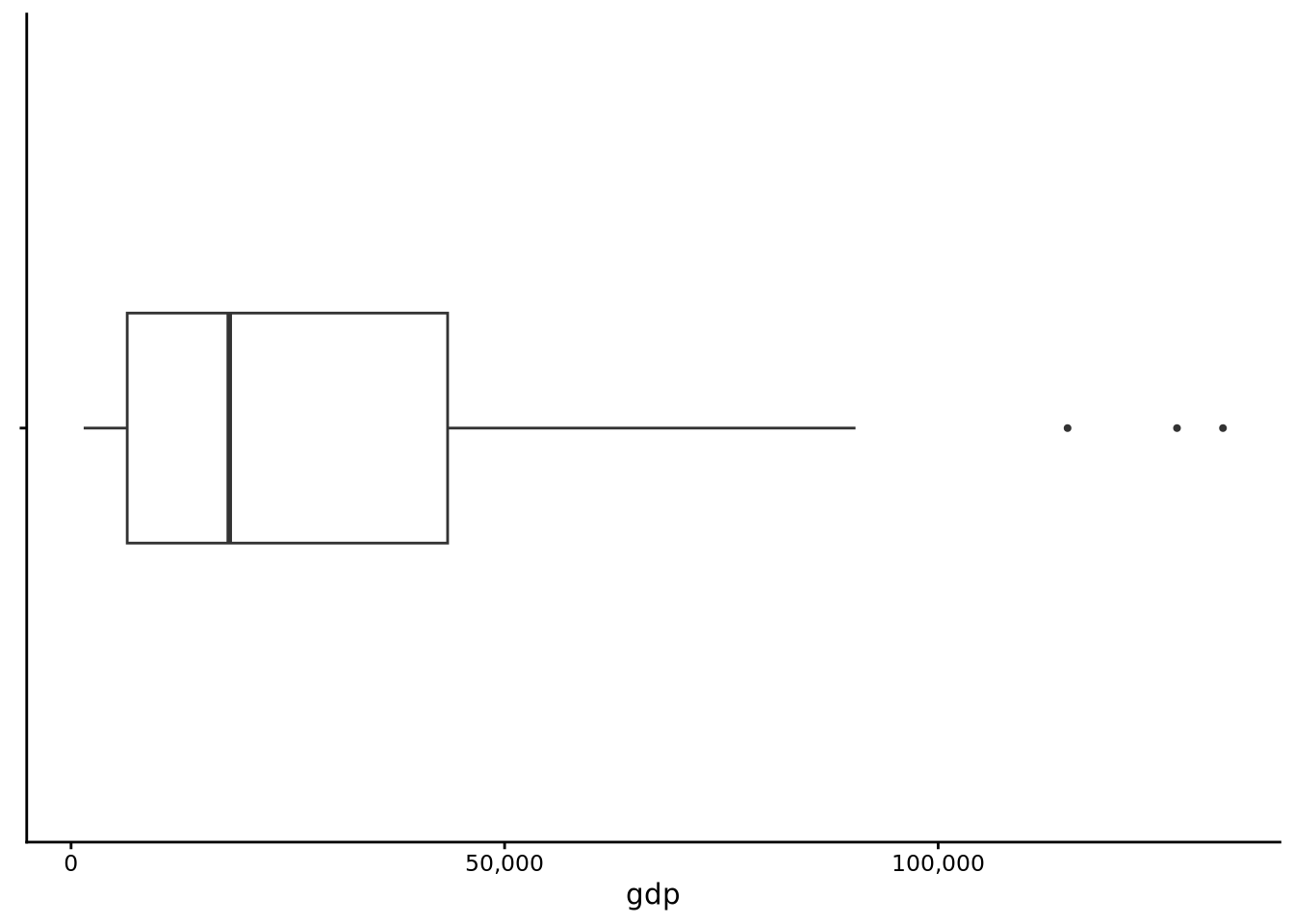
Here the picture changes considerably. The median is somewhere around $20,000, yet the upper whisker runs far to the right and a string of outlier dots climbs even higher. Most countries cluster in a comparatively narrow box on the low-income side, but a handful reach well past $60k. In other words, half of all countries are at or below around $20,000, and the other half are stretched out between $20,000 and well over $100,000. This confirms the long upper tail we saw in the GDP histogram: a small group of very wealthy nations pulls the upper tail far from the centre, while very low GDP values are rare enough not to appear as separate outliers on the left.
The Tukey boxplot is a simple plot. It could even be sketched by hand after a few calculations, but it is highly informative. It packs the centre, spread, and shape (asymmetry, tails) into a single compact graphic. In one glance we learned that happiness scores are fairly symmetric with a mild left tail, whereas GDP is highly asymmetric to the right and dotted with extreme high earners. Those impressions will guide the numeric summaries we develop in the next section.
3.5 Descriptive statistics
The histograms and boxplots you have just drawn are not mere decoration; they already told us a great deal. At a glance we could see where most countries sit on the happiness scale, how tightly (or loosely) those scores bunch together, and whether the distribution leans to one side or sprouts a long tail. Visuals excel at revealing patterns quickly and at alerting us to oddities; an unexpected cluster, an outlying dot, a lopsided tail. Yet pictures alone cannot answer every practical question. If we want to precisely compare two datasets, report the major features of a distribution in a compact form, we also need numbers.
Descriptive statistics, often called summary statistics, do that numerical condensing. Just as our plots highlighted three visual cues, the numbers we compute will home in on three parallel facets:
- central tendency: the point around which the data cluster;
- spread or variability: how far observations stray from that centre;
- shape: everything else, particularly asymmetry (skewness) and the weight of the tails versus the middle (kurtosis)
The goal is the same: capture the most salient features of a variable, this time in a handful of well-chosen values.
3.5.1 Central Tendency
We will first focus on three measures of central tendency: the mean, the median and the mode.
3.5.1.1 Mean
When most people say “average,” they in fact mean the mean (or arithmetic mean, to be even more precise). The mean is calculated as the sum of all values divided by the number of values. Intuitively, the mean is the centre of gravity of the distribution of points. But this is not merely an analogy; the mean is literally the centre of gravity of the data.
Imagine each observation as a small, equal-weight bead on a long stick or ruler. Lay the ruler on a pivot, the fulcrum, and move that fulcrum left or right until the ruler balances and sits level. The spot where it balances is exactly the mean. Mathematically, the distances of beads to the left of the mean exactly counterbalance the distances of beads to the right. If you shift a single bead farther out in one direction, you must move the fulcrum toward it to keep everything level.
Let’s calculate the mean with R. For this, we will use the summarise() function that is part of dplyr, and so loaded if the tidyverse is loaded. As we will see, the summarise() function is a general-purpose tool for calculating any descriptive statistics. In the following line, inside summarise, we use mean(), which is R’s function for calculating the mean, to calculate the mean of happiness:
summarise(whr2025, mean_happiness = mean(happiness))# A tibble: 1 × 1
mean_happiness
<dbl>
1 5.55The output as you can see is a data frame (another tibble) with just one row and one column named mean_happiness. If we wanted to name that column differently, we could easily do so, for example:
summarise(whr2025, average_happiness = mean(happiness))# A tibble: 1 × 1
average_happiness
<dbl>
1 5.55The histograms and boxplots we drew earlier make the meaning of the mean more concrete. In the happiness histogram, most bars sit close to the middle of the scale, so the balance point lands near 6; a few countries down around 2 tug the mean leftward, but not by much because they are relatively light ballast compared with the many mid-range bars.
For comparison, let’s look at gdp.
summarise(whr2025, mean_gdp = mean(gdp))# A tibble: 1 × 1
mean_gdp
<dbl>
1 27385.Notice how this mean value of $27385 is noticeably higher than the midpoint of the box in the boxplot for gdp. For gdp, there is a huge stack of countries with modest incomes and a long tail of very high incomes. Those high-income countries act like beads fixed far out on the right side of the ruler, forcing the mean well beyond the bulk of the data.
As an aside, notice how the mean of gdp is displayed as 27385. without any digits shown in the decimal part of the value. This is the default behaviour of tibbles to show decimal digits to a set number of significant figures rather than decimal places (see Note 3.5). If you would like to see a fixed number of decimal places, you can pipe (see Section 2.7.4) the output to the to_fixed_digits() function supplied with sgsur:
summarise(whr2025, mean_gdp = mean(gdp)) |>
to_fixed_digits()# A tibble: 1 × 1
mean_gdp
<num:.3!>
1 27384.525We explained earlier that tibbles are just data frames but print out the data differently. One of the rules it follows is that it does not show a fixed number of decimal places. It has good reason for this. Data frames often mix tiny and huge numbers. If we insisted on, say, four places after the decimal, the large value would sprout a long train of zeros (e.g. 250000.0000), widening the column and forcing other columns to wrap or disappear. Conversely, choosing a small fixed width would chop useful detail off small numbers. In addition, many numbers are measurements that are accurate only to a handful of significant digits. Printing “250000.0000” suggests precision that may simply not be there. In any case, for very large numbers, the trailing digits are practically uninformative relative to the integer part.
If every value looks like a whole number (no meaningful digits after the decimal), the tibble shows the entire integer exactly:
tibble(x = 123456789)# A tibble: 1 × 1
x
<dbl>
1 123456789For numbers that do have decimal detail, the tibble shows only the first few significant digits (three by default) and rounds the rest away:
tibble(x = 123.456789)# A tibble: 1 × 1
x
<dbl>
1 123.A trailing dot reminds you the stored value is still a decimal number, not an integer.
You can ask for more (or fewer) significant figures with
options(pillar.sigfig = 5)
# now prints 5 significant figures
tibble(x = 123.456789)# A tibble: 1 × 1
x
<dbl>
1 123.46If you prefer to override this behaviour of tibbles and see a fixed number of decimal places instead, you can use the to_fixed_digits() function from the sgsur package. By default, this will show the number rounded to three decimal places:
tibble(x = 123.456789) |> to_fixed_digits()# A tibble: 1 × 1
x
<num:.3!>
1 123.457And you can control the number of decimal places shown by setting the value of .digits, e.g.
tibble(x = 123.456789) |> to_fixed_digits(.digits = 2)# A tibble: 1 × 1
x
<num:.2!>
1 123.46Although the mean is a simple calculation, and one that is easy to describe in words (the sum of all values divided by the number of values), let us take this opportunity to look at its formula, which is the first statistical formula we will meet in this book. As mentioned in Chapter 1, we will keep formulas to a minimum in this book, but there will be a few. This is necessary in order to explain some calculations and techniques precisely and without ambiguity.
Let’s say we are calculating the mean of some variable \(x\), which could be the happiness or gdp values in whr2025. In general, we can say that the variable \(x\) is the set of values \[
x_1, x_2, x_3 \ldots x_n.
\] Here, \(x_1\) (read as “x sub 1” or “x subscript 1”) refers to the first data value, \(x_2\) refers to the second data value, and so on. The subscripts act like an index. They tell us which specific data point we are talking about. Think of them like position numbers in a list:
- \(x_1\) = the 1st value
- \(x_2\) = the 2nd value
- \(x_3\) = the 3rd value
The ellipsis (…) means “and so on”, indicating there are more values in between that we are not writing out. The final term \(x_n\) represents the last data value, where \(n\) is the total number of observations. So if we have 139 countries in whr2025, then \(n = 139\) and \(x_{139}\) is the happiness score of the final country in the set.
The mean of \(x = x_1, x_2, x_3 \ldots x_n\) is typically referred to as \(\bar{x}\), pronounced “x bar”. We can write the formal definition of the mean as follows: \[ \bar{x} = \dfrac{1}{n} \displaystyle\sum_{i=1} ^n x_i. \]
Although this formula might look a little daunting on first inspection, we will work through it together and see that it is just a set of instructions that tell us how to use our data to calculate the mean. The large \(\Sigma\), pronounced (uppercase) “sigma”, means take the sum and the \(x_i\) next to it tells us what we need to take the sum of; in this case \(x_i\) refers to each value of the variable \(x\). On the bottom of \(\Sigma\), we have \(i=1\) and at the top, we have \(n\). These are known as the limits of the sum. They mean that the value of \(i\) in \(x_i\) goes from \(i=1\) to \(i=n\). In other words, \[ \displaystyle\sum_{i=1} ^n x_i = x_1 + x_2 + x_3 + \ldots + x_n. \] While we could always write a sum out the long way, the notation \(\sum_{i=1} ^n x_i\) means the exact same thing but is much more compact.
The next step is to divide the sum of all values in the variable by the number of values. This could be written like the following: \[ \bar{x} = \dfrac{\sum_{i=1} ^n x_i}{n} \]
However, it is typically written in the form shown above: \[ \dfrac{1}{n} \displaystyle\sum_{i=1} ^n x_i. \]
These two formulas are identical. In the latter case, instead of writing it as dividing the sum of all the observations by \(n\), we multiply by \(\dfrac{1}{n}\), which gives the same result.
Let’s work through the formula using a small example, the number of times six people check their phones in an hour:
x <- c(12, 4, 27, 1, 22, 30)
x[1] 12 4 27 1 22 30Here, the c() function is just R’s way of creating a set of values. In other words, in the code, x is the set, properly known as a vector, of values \(12, 4, 27, 1, 22, 30\). This x is not a data frame, but is equivalent to a column of a data frame.
The mean for x is: \(\bar{x} = \dfrac{1}{6} \displaystyle\sum_{i=1} ^6 x_i\) and this is calculated as follows: \[
\begin{aligned}
\bar{x} &= \dfrac{1}{6} (12 + 4 + 27 + 1 + 22 + 30),\\
&= \dfrac{1}{6} 96,\\
&= 16
\end{aligned}
\]
Using R, we can calculate the mean using the mean function:
mean(x)[1] 163.5.1.2 Median
Whilst the mean is a hugely useful tool — telling us the centre of gravity of a distribution — it does have a weakness: it is extremely sensitive to outliers.
Let’s revisit our phone-checking example; we will add a seventh observation to our set:
x_alt <- c(12, 4, 27, 1, 22, 30, 650)
x_alt[1] 12 4 27 1 22 30 650Now when we calculate the mean, we observe that the mean is greatly increased (from 16, the mean of x):
mean(x_alt)[1] 106.5714We can see here that the mean has been highly influenced by the inclusion of the high seventh value. The take-home message here is that the mean is highly sensitive to extreme values, and so in these cases other measures of central tendency, such as the median, should be considered.
The median is the middle value of a set of values when they are placed in ascending order. In the case of x_alt, the sorted values are: 1, 4, 12, 22, 27, 30, 650, and so the median is the middle value: 22. Note how the influence of the extreme value is much less and that the median represents a typical value of the set much better than the mean (106.57).
We calculate the median slightly differently if there are an odd or even number of observations.
Odd number of observations
We have the following observations, placed in ascending order:
\[ 2, 3, 5, 8, 9, 10, 120 \]
The median here is the middle number, 8, which has exactly three values higher and three values lower. Note how the median of 8 is typical of the majority of these values even though we have one extreme value of 120
Even number of observations
When we have an even number of observations, we find the two points that are in the middle of the list. Here, that is 8 and 9.
\[ 2, 3, 5, 8, 9, 10, 12, 150 \]
We then take the mean of these two numbers, which gives us our median, 8.5.
In R, we calculate the median with the median() function. For example, the median of x_alt is
median(x_alt)[1] 22The median is often referred to as a robust measure of central tendency because it is not sensitive to extreme values in the data. If the extreme values of a set increase, so too will the mean, but the median will not change. For example, if we increase the extreme value in the x_alt set from 650 to 6500 to 65000 to 650000, the resulting means are 106.57, 942.29, 9299.43, 92870.86. By contrast, the resulting medians remain the same: 22.
Let us now calculate the median happiness score of our whr2025 data. Again, we can use the summarise() function, this time using median() instead of mean():
summarise(whr2025, median_happiness = median(happiness))# A tibble: 1 × 1
median_happiness
<dbl>
1 5.82We can use summarise() to see the mean and median of happiness side by side (here, we break the code over multiple lines for readability; see Section 2.8.5).
summarise(whr2025,
mean_happiness = mean(happiness),
median_happiness = median(happiness))# A tibble: 1 × 2
mean_happiness median_happiness
<dbl> <dbl>
1 5.55 5.82These are quite close but the mean is lower than the median, reflecting the slightly longer tail to the left.
For comparison, let us look at gdp.
summarise(whr2025,
mean_gdp = mean(gdp),
median_gdp = median(gdp))# A tibble: 1 × 2
mean_gdp median_gdp
<dbl> <dbl>
1 27385. 18244.In this case, the mean is considerably higher than the median. The high mean reflects the long right tail stretching up to very high average incomes.
In general, the median better represents the “typical” value than the mean. With the median, it is always the case that 50% of values are above it, and 50% are below. The median answers the question “what value splits my data in half?” while the mean answers “what’s the mathematical centre of gravity?” The centre of gravity is unduly influenced by goings-on at the extreme, while the median is not. These two can be quite different things when your data is not evenly spread out.
3.5.1.3 The mode
The mode of a distribution is the value that occurs most frequently. For some variables calculating the mode is very straightforward, but for others it is not.
For starters, let’s look at the income variable in whr2025. When we used skim in Section 3.2, we saw that income has three distinct values: low, medium, high. We can use the count() function from dplyr to tally how often each value appears:
count(whr2025, income)# A tibble: 3 × 2
income n
<ord> <int>
1 low 47
2 medium 46
3 high 46From this table we can clearly see which of the three levels occurs most often.
R has no built-in function for the statistical mode (the function mode() refers to how an object is stored in memory so is not relevant). The sgsur package supplies get_mode(), which returns the most frequent value (or values, if there is a tie) and its frequency:
get_mode(whr2025, income)# A tibble: 1 × 2
income count
<ord> <int>
1 low 47Calculating the mode for numeric data is harder. With continuous variables many, or even all, values occur only once, so in practice there is no mode. Counting the occurrences of each happiness value illustrates this point:
count(whr2025, happiness)# A tibble: 136 × 2
happiness n
<dbl> <int>
1 1.72 1
2 3.19 1
3 3.24 1
4 3.30 1
5 3.34 1
6 3.38 1
7 3.42 1
8 3.50 2
9 3.57 1
10 3.78 1
# ℹ 126 more rowsAlmost every score is unique.
If you still want a “mode” for a continuous variable, one workaround is to bin the data into equal-width groups and pick the bin with the largest count. The function get_binned_mode() from sgsur does this:
get_binned_mode(whr2025, happiness)# A tibble: 1 × 2
happiness count
<dbl> <int>
1 6.20 33By default the function uses ten bins. It returns the midpoint of the fullest bin, which in this case is 6.2.
Changing the bin count changes the answer:
get_binned_mode(whr2025, happiness, n_bins = 5) # five bins# A tibble: 1 × 2
happiness count
<dbl> <int>
1 6.00 54get_binned_mode(whr2025, happiness, n_bins = 20) # twenty bins# A tibble: 1 × 2
happiness count
<dbl> <int>
1 6.05 18For happiness the midpoint moves only slightly, but the choice of bins can matter a great deal, as the skewed gdp variable shows:
get_binned_mode(whr2025, gdp, n_bins = 5)# A tibble: 1 × 2
gdp count
<dbl> <int>
1 10635. 87get_binned_mode(whr2025, gdp, n_bins = 20)# A tibble: 1 × 2
gdp count
<dbl> <int>
1 3989. 39Whether the mode is near $11,000 or $4,000 depends entirely on an arbitrary bin width.
The takeaway is that a mode is well defined and occasionally useful when a variable has only a small set of discrete values. For genuinely continuous data the concept breaks down because any “mode” you report hinges on how you bin the variable, so it is usually better to rely on other summaries of central tendency such as the mean or median.
3.5.2 Dispersion
In addition to understanding the centre, or averageness, of a variable of interest, it is also important that we understand how observations are spread around this centre. For example, do most observations tend to fall close to the centre, or are they more spread out? This is known as dispersion (or variability, or spread). There are several descriptive statistics that measure dispersion.
3.5.2.1 Range
The simplest measure of dispersion is the range, which is simply the difference between the largest observation and the smallest observation. This tells us exactly how much variability there is in the data by giving us the distance between the minimum and maximum values.
In terms of terminology, sometimes the term range is used to denote the two endpoints, the minimum and maximum, of a set of values. Other times, and probably more correctly, the term range refers to the distance between these two endpoints, which is how we use the term here. In R, the built-in range() function returns the minimum and maximum values, rather than the difference between them. However, the get_range() function in sgsur returns that difference.
In the following code we find the range of happiness in the whr2025 data using the get_range() function inside summarise():
summarise(whr2025, range = get_range(happiness))# A tibble: 1 × 1
range
<dbl>
1 6.02For gdp, the range is as follows:
summarise(whr2025, range = get_range(gdp))# A tibble: 1 × 1
range
<dbl>
1 131391.Just like the mean, the range is not robust to extreme values. A few unusually large or small observations can inflate it even when most of the data are tightly clustered.
3.5.2.2 Interquartile Range (IQR) and friends
A more robust alternative to the range is the inter-quartile range (IQR), introduced earlier when we discussed boxplots. The IQR describes the spread of the middle 50% of the data and is far less sensitive to extreme points.
We calculate the IQR by first finding the 25th percentile (Q1) and the 75th percentile (Q3). These are the points below which lie 25% and 75% of the values, respectively. Subtracting Q1 from Q3 gives the IQR. In R, the function IQR() calculates the inter-quartile range, and here we use it inside summarise():
summarise(whr2025, iqr = IQR(happiness))# A tibble: 1 × 1
iqr
<dbl>
1 1.60The idea behind the IQR can be stretched further. Instead of always using the 25th and 75th percentiles, we can choose any pair of symmetric percentiles around the median. That means picking a percentile below 50% and pairing it with its mirror above 50%. Think of it as zooming in or out on the “middle chunk” of the data.
Formally, let \(p\) be such a proportion. The distance between the \((100p)\)-th percentile and the \((100(1-p))\)-th percentile is called an inter-percentile range (IPR).
For example: - If \(p = 0.25\), the range spans from the 25th to the 75th percentile. This is the familiar inter-quartile range (IQR), covering the middle 50% of the data. - If \(p = 0.10\), the range spans from the 10th to the 90th percentile. This gives the inter-decile range (IDR), the middle 80% of the data. - If \(p = \tfrac{1}{3}\), the range spans from the 33rd to the 67th percentile. This gives the inter-tercile range (ITR), the middle third of the data on each side.
These inter-percentile ranges are all variations on the same idea: measuring how wide a central slice of the distribution is. The smaller the slice (larger \(p\)), the more tightly you zoom in on the centre. The larger the slice (smaller \(p\)), the more of the tails you include.
The sgsur package provides a general helper ipr() together with convenience wrappers idr() and itr(). You can compute any of these inter-percentile ranges inside a summarise() call, just as you would the IQR.
# happiness: central 80 %, 50 %, and 66.7 %
summarise(whr2025,
idr_happiness = idr(happiness), # p = 0.10
iqr_happiness = IQR(happiness), # p = 0.25
itr_happiness = itr(happiness)) # p = 1/3# A tibble: 1 × 3
idr_happiness iqr_happiness itr_happiness
<dbl> <dbl> <dbl>
1 2.94 1.60 1.08# gdp: the same three bandwidths
summarise(whr2025,
idr_gdp = idr(gdp),
iqr_gdp = IQR(gdp),
itr_gdp = itr(gdp))# A tibble: 1 × 3
idr_gdp iqr_gdp itr_gdp
<dbl> <dbl> <dbl>
1 60303. 36951. 24602.You can adjust p in ipr() to define any other central band you need. For example, the middle 90 % of happiness scores:
summarise(whr2025,
ipr90_happiness = ipr(happiness, p = 0.05))# A tibble: 1 × 1
ipr90_happiness
<dbl>
1 3.65Each statistic tells you how wide the chosen central slice of the distribution is, with smaller \(p\) capturing more of the tails and therefore producing a larger range.
3.5.2.3 Variance & Standard deviation
The variance and standard deviation are two of the most widely used measures of statistical dispersion. The formal definition of the variance is as follows: \[ \text{variance}= \dfrac{1}{n-1} \displaystyle\sum_{i=1} ^n (x_i - \bar{x})^2. \] At first sight this may look intimidating, but remember, formulas are really just a set of instructions. - As we saw earlier when discussing sums, \(\Sigma\) means “sum up.” - The little \(i = 1\) at the bottom and \(n\) at the top tell us the range: start with the first observation (\(x_1\)), keep going through \(x_2, - x_3, …\), all the way to the last one (\(x_n\)). - Inside the brackets, \((x_i - \bar{x})\) means: take each observation \(x_i\) and subtract the mean \(\bar{x}\). This gives the deviation of each - point from the mean. - We then square these deviations so that negative and positive gaps don’t cancel out. - Add up all of these squared deviations (that’s what the \(\Sigma\) does). - Finally, divide by \(n-1\) to get the average squared deviation. - The result is the variance: a single number that captures how spread out the data are around their mean.
Let’s work through the formula using the fictitious data from earlier that gave the number of times individuals check their phone in an hour:
x[1] 12 4 27 1 22 30The mean of this data is 16, so the variance is calculated as follows: \[ \text{variance}= \dfrac{1}{6-1} \displaystyle\sum_{i=1} ^6 (x_i - 16)^2. \]
This works out as follows: \[ \begin{aligned} \text{variance} &= \dfrac{1}{5} \displaystyle\sum_{i=1} ^6 [(12 - 16)^2 + (4 - 16)^2 + (27 - 16)^2 + (1 - 16)^2 + (22 - 16)^2 + (30 - 16)^2],\\ &= \dfrac{1}{5} [16 + 144 + 121 + 225 + 36 + 196],\\ &=\dfrac{1}{5} [738],\\ &=147.6. \end{aligned} \]
We can verify this by calculating the variance using R’s var function:
var(x)[1] 147.6We can calculate the variance of happiness in the whr2025 data in R as follows:
summarise(whr2025, variance = var(happiness))# A tibble: 1 × 1
variance
<dbl>
1 1.32On its own, the variance is not particularly intuitive to interpret. Because we needed to include the square term in the calculation, the variance is not calculated on the same scale as the original variable. As such, in order to reverse the squaring, we simply take the square root of the variance, which gives us a very widely used measure of variability, the standard deviation. The formal definition of the standard deviation of a variable \(x\) is just the square root of the variance of \(x\): \[ \text{standard deviation}= \sqrt{\dfrac{1}{n-1} \displaystyle\sum_{i=1} ^n (x_i - \bar{x})^2}. \]
The standard deviation is calculated in R with sd():
summarise(whr2025,
happiness_sd = sd(happiness),
gdp_sd = sd(gdp))# A tibble: 1 × 2
happiness_sd gdp_sd
<dbl> <dbl>
1 1.15 26279.The standard deviation is best thought of as the typical distance of a data point from the mean. It is a single, interpretable number on the same scale as the data: seconds for reaction times, pounds for income, points for happiness.
A small standard deviation means most observations huddle close to the mean; a large one means they wander farther afield. When a variable is roughly bell-shaped, we can make even more precise rules of thumb: about two-thirds of values lie within one standard deviation of the mean, about 95% within two, and almost all (99% or more) within three. These “68–95–99” benchmarks let you look at a histogram, note the standard deviation, and immediately gauge where the bulk of the distribution should fall. Even when the data are not bell-shaped, the standard deviation still carries guaranteed information (see Note 3.7).
Formal mathematical results tell us that for any distribution, at least \(1-1/k^{2}\) of the observations must lie within \(k\) standard deviations of the mean. Thus, at least \(1 - \dfrac{1}{2^2} = 1-\dfrac{1}{4}=75\%\) of values are always within \(k=2\) standard deviations, at least 89% within \(k=3\), and at least 94% within \(k=4\). These lower bounds are conservative — the actual areas within \(k\) standard deviations could be much higher — yet they show why the standard deviation remains useful in all distributions: it sets a scale that limits how far most of the data can stray.
The variance, which is simply the average of the squared gaps before taking that final square root, is less intuitive to read because it lives in squared units, but it underpins the algebra of many statistical methods. In day-to-day work, though, the standard deviation is the number that tells you, in the data’s own language, how tightly or loosely the values gather around their centre.
3.5.2.4 Median absolute deviation
A final measure of dispersion to consider is the median absolute deviation (MAD). For a variable \(x\) with sample median \(\tilde{x}\), the MAD is defined as \[ \operatorname{MAD}(x)=\operatorname{median}\bigl(\lvert x_{i}-\tilde{x}\rvert\bigr), \]
Here is what this means in practice: - Start with the median of the dataset, \(\tilde{x}\). - For each observation \(x_i\), calculate its distance from the median: \((x_i - \tilde{x})\). - Apply the absolute value \(\lvert \cdot \rvert\), which means “ignore the sign.” - If the difference is positive, keep it as it is. - If the difference is negative, flip it to positive. - For example: \(\lvert 5 - 8\rvert = \lvert -3\rvert = 3\), and \(\lvert 12 - 8\rvert = \lvert 4\rvert = 4\). - The absolute value makes sure we are measuring distance only, not direction. - Finally, take the median of all these distances.
That value is the MAD: the median distance of each observation from the median of the data. Because it is anchored on the median and uses absolute (not squared) gaps, a single extreme value can move the MAD only so far: it is much less sensitive to outliers than either the variance or the standard deviation. Just as the median is a robust counterpart to the mean, the MAD is a robust counterpart to the standard deviation.
In R, the mad() function computes this quantity. By default, it multiplies the raw MAD by \(1.4826\), a constant that makes the result agree, on average, with the standard deviation when the data are perfectly normal. You can turn off that rescaling by setting constant = 1 when you call mad().
The MAD for happiness and gdp illustrates how the statistic resists the extreme right tail in income:
# default constant = 1.4826: scaled to match sd for a normal distribution
summarise(whr2025,
mad_happiness = mad(happiness),
mad_gdp = mad(gdp))# A tibble: 1 × 2
mad_happiness mad_gdp
<dbl> <dbl>
1 1.18 21532.# raw, unscaled MAD (constant = 1)
summarise(whr2025,
raw_mad_happiness = mad(happiness, constant = 1),
raw_mad_gdp = mad(gdp, constant = 1))# A tibble: 1 × 2
raw_mad_happiness raw_mad_gdp
<dbl> <dbl>
1 0.795 14523.For happiness the scaled MAD is close to the standard deviation, as theory predicts for bell-shaped data, while for the strongly skewed gdp it stays far below the standard deviation, confirming its robustness. In practice, you can quote the default, scaled MAD when you want a robust measure of dispersion that is still on the same footing as the standard deviation, or use the raw version when you prefer the literal median of absolute deviations.
3.5.3 Shape
Once centre and dispersion are described, shape is everything that remains. It describes how data are arranged beyond simply “where” and “how wide.” In practice, we usually concentrate on two facets:
- symmetry: whether the distribution balances evenly to the left and right of the centre or leans more to one side
- tail weight: how much probability lives in the tails compared with a standard bell-shaped distribution; do the tails drop away quickly, or do the values linger out in the distance?
Skewness and kurtosis give us numerical descriptions of these two concepts, respectively.
Many real-world variables — heights, test scores, birth weights — often cluster around a central value, tapering off evenly in both directions. That means most people (or observations) have values close to the average, with fewer and fewer as you move further away in either direction. When plotted, this creates the familiar bell-shaped curve, also called the normal distribution.
Key features: - Symmetry: the left and right halves are mirror images. - Centre: the mean, median, and mode all coincide at the peak. - Spread: most observations (about two-thirds) fall within one standard deviation of the mean, about 95% within two, and almost all within three. - Tails: the curve thins smoothly as you move away from the centre, but technically never touches zero — extreme values are always possible, just very rare.
Why it matters: The normal distribution underpins much of classical statistics. It provides simple mathematical rules that approximate many real datasets well, and it serves as a reference point for concepts like standard deviation, z-scores, and hypothesis testing.
Not everything in the world is normal, but understanding the bell-shaped curve gives you a benchmark against which other shapes (skewed, heavy-tailed, etc.) can be compared.
3.5.3.1 Skewness
Skewness quantifies asymmetry:
- A positive value means a right-skewed distribution: the right-hand (upper) tail is longer than the left.
- A negative value means a left-skewed distribution: the left-hand (lower) tail is the longer one.
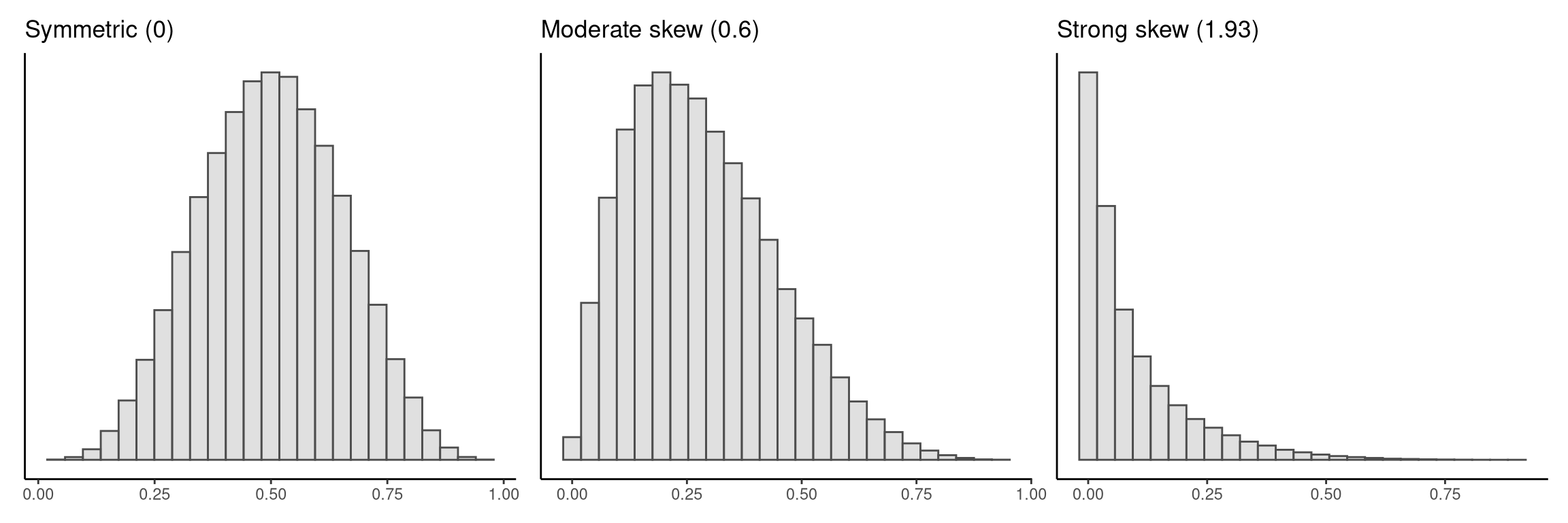
The sign of the skewness tells us whether it is positive/right or negative/left. Rules of thumb for the interpretation of the absolute value (value regardless of sign) of the skewness are as follows:
- Between 0.0 and 0.5: essentially symmetric
- Between 0.5 and 1.0: moderately skewed
- Greater than 1.0: strongly skewed
For example, a value of \(-1.5\) means a strong negative or left skew, and a value of \(0.7\) means a moderate positive or right skew. See Figure 3.9 for illustrations of symmetric and moderately or strongly skewed distributions.
A common shortcut says if “mean > median \(\implies\) right skew; mean < median \(\implies\) left skew.” That relationship is only a tendency, not a law. Counter-examples exist, and Hippel (2005) explains why the textbook rule needs caveats. However, it is still a useful rule of thumb so long as it is treated as such rather than a hard rule.
The skewness() function in sgsur (imported from the moments package) computes the standard coefficient of skewness used in statistics. Here, we calculate the skewness of happiness and gdp:
summarise(whr2025,
skew_happiness = skewness(happiness),
skew_gdp = skewness(gdp))# A tibble: 1 × 2
skew_happiness skew_gdp
<dbl> <dbl>
1 -0.494 1.47As we can see, happiness shows moderate left skew (negative sign), whereas gdp is strongly right-skewed (positive sign). This closely matches what we can see visually using the histograms and boxplots.
3.5.3.2 Kurtosis
Kurtosis measures how heavy the tails are relative to a typical bell-shaped distribution (specifically, a normal distribution, see Chapter 6). Kurtosis is sometimes misdescribed as a measure of “peakedness,” but the statistic tells us almost nothing about how pointy or flat the centre is; it reflects the weight of the tails. Westfall (2014) reviews the history of this misconception and shows that only a small fraction of the kurtosis value comes from the central region, so kurtosis should be interpreted strictly in terms of tail heaviness.
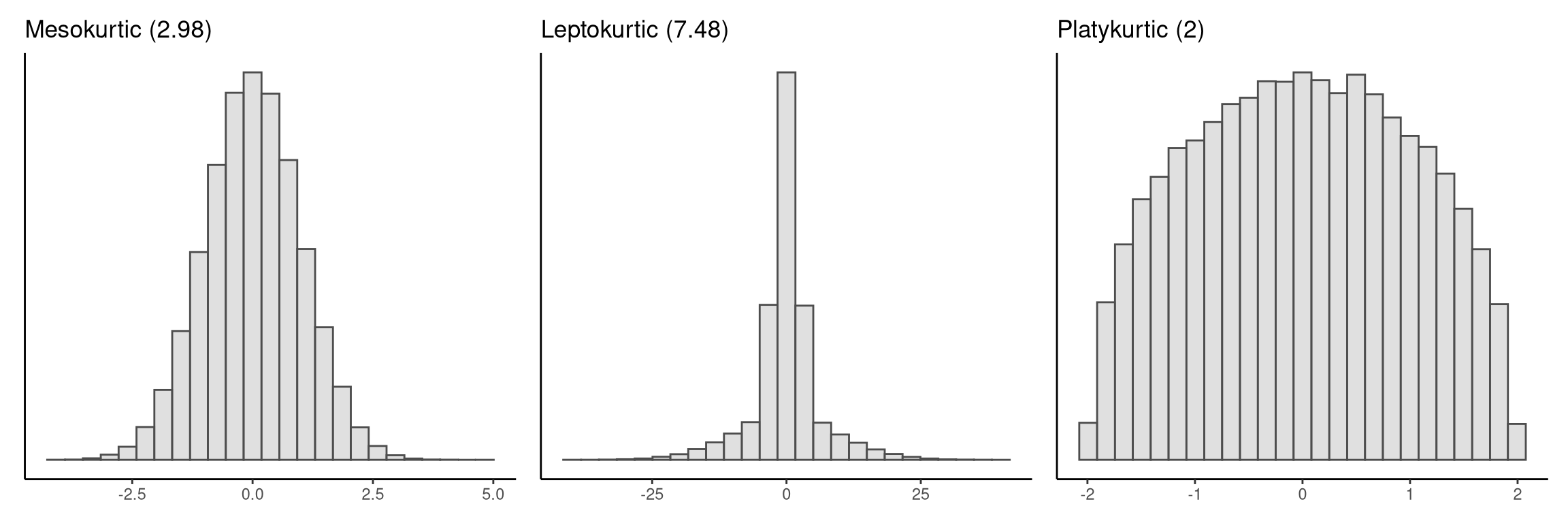
A normal distribution has a kurtosis of 3 exactly. Because 3 is an inconvenient baseline, many authors redefine kurtosis by subtracting 3. When this is done, the original kurtosis value is then sometimes called raw kurtosis, while the adjusted value is excess kurtosis.
In the following table, we have the common interpretation of kurtosis value, expressed in terms of both raw and excess kurtosis values:
| Excess kurtosis | Raw kurtosis | Tail description | Kurtosis regime |
|---|---|---|---|
| ≈ 0 | ≈ 3 | Normal-like tails | Mesokurtic |
| > 0 | > 3 | Heavy tails | Leptokurtic |
| < 0 | < 3 | Light tails | Platykurtic |
Positive excess kurtosis (leptokurtic) signals data that generate more extreme values than the normal curve predicts. Negative excess kurtosis (platykurtic) signals tails that drop off more quickly. See Figure 3.10 for illustration of mesokurtic, leptokurtic, and platykurtic distributions.
The function kurtosis() in the sgsur package calculates kurtosis, and by default it returns the raw kurtosis value. Here, we use it in the summarise() function to calculate the kurtosis of happiness and gdp:
summarise(whr2025,
kurt_happiness = kurtosis(happiness), # raw kurtosis
kurt_gdp = kurtosis(gdp))# A tibble: 1 × 2
kurt_happiness kurt_gdp
<dbl> <dbl>
1 2.81 5.49If we want to obtain the excess kurtosis value instead, then we set excess = TRUE in the kurtosis() function (by default, excess = FALSE):
summarise(whr2025,
kurt_happiness = kurtosis(happiness, excess = TRUE), # excess kurtosis
kurt_gdp = kurtosis(gdp, excess = TRUE))# A tibble: 1 × 2
kurt_happiness kurt_gdp
<dbl> <dbl>
1 -0.188 2.49Using the common interpretations, happiness sits close to the normal benchmark, while the positive excess kurtosis for gdp confirms the very heavy upper tail.
Kurtosis is practically important because in heavy-tailed distributions, extreme events are unlikely but not astronomically unlikely. In financial risk modelling, for example, assuming normal tails can underestimate the probability of very large losses. This underestimation has been cited as one ingredient in the 2007–2008 global financial crisis (see Taleb (2007) for a discussion aimed at practitioners). Positive excess kurtosis is a quick numerical flag that a model based on thin normal tails may miss important risk in the extremes.
3.6 Exploring relationships
Up to this point we have treated each variable in isolation; drawing a histogram or boxplot of happiness, calculating its mean or standard deviation, and so on. Those visualisations and summaries are essential, and from them we have already learned a lot about how happiness and gdp are distributed across countries. However, treating each variable in isolation leaves an obvious question unanswered: How does one variable behave when another variable changes? In other words, what can we learn from the relationships between variables?
3.6.1 Visualising conditional distributions
A first step is to compare the distribution of a numeric variable within separate levels of a discrete variable. Statisticians call such comparisons conditional, stratified, or simply grouped summaries.
The two visualisation functions we have used so far — histogram() and tukeyboxplot() — both let us explore conditional patterns. For instance, we can compare life satisfaction scores across the three income tiers by drawing a separate boxplot for each tier:
tukeyboxplot(happiness, x = income, data = whr2025)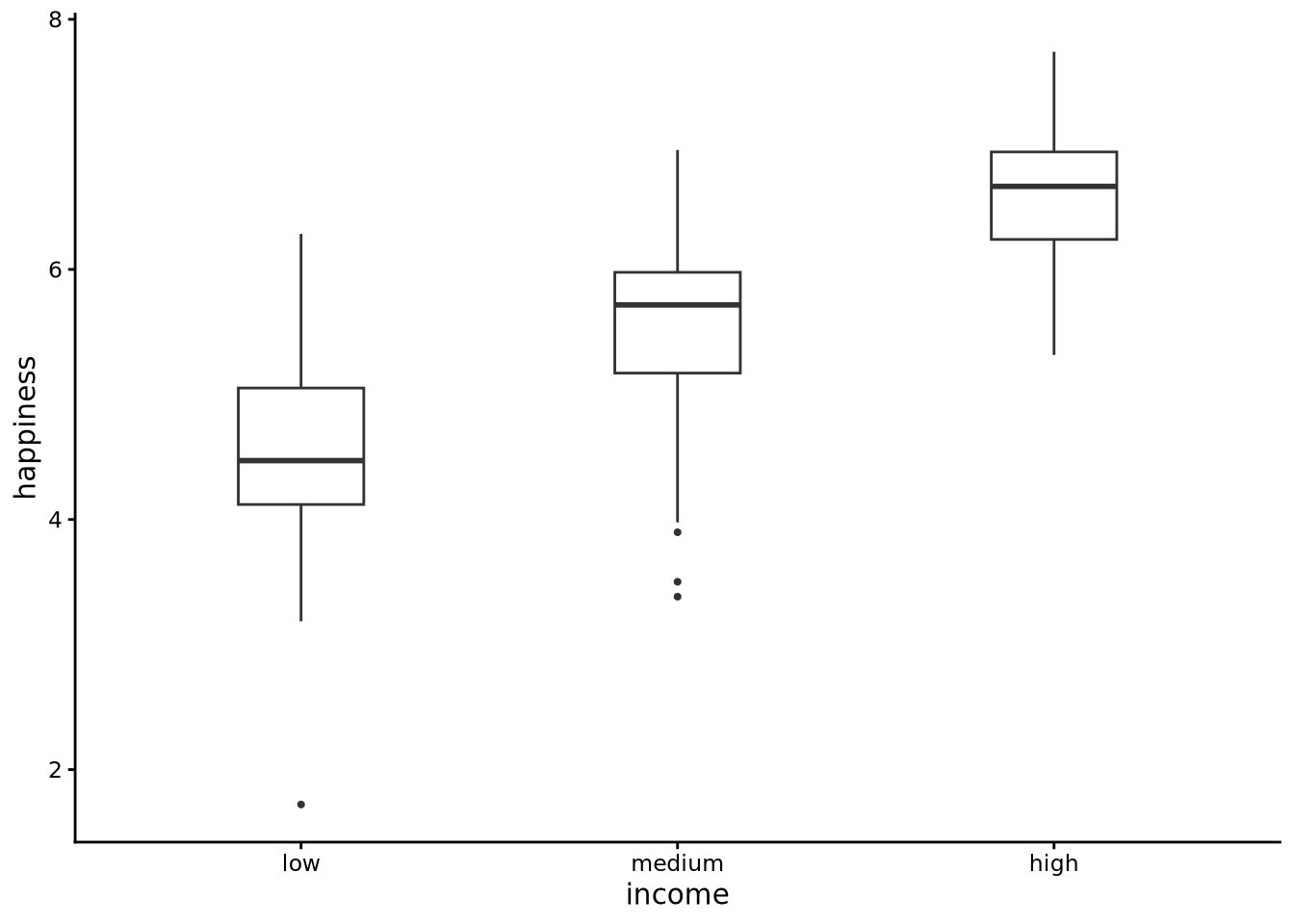
Each boxplot is read in the usual way (median line, IQR box, whiskers, and outliers), but now the left-hand box summarises happiness among low-income countries, the middle box covers the medium-income group, and the right-hand box shows the high-income group. Side by side, the three panels reveal how the centre, spread, and tails of the happiness distribution shift as national income rises.
We can easily make conditional histograms with the histogram() function. For example, in the following, we make a stacked histogram:
histogram(happiness, by = income, data = whr2025)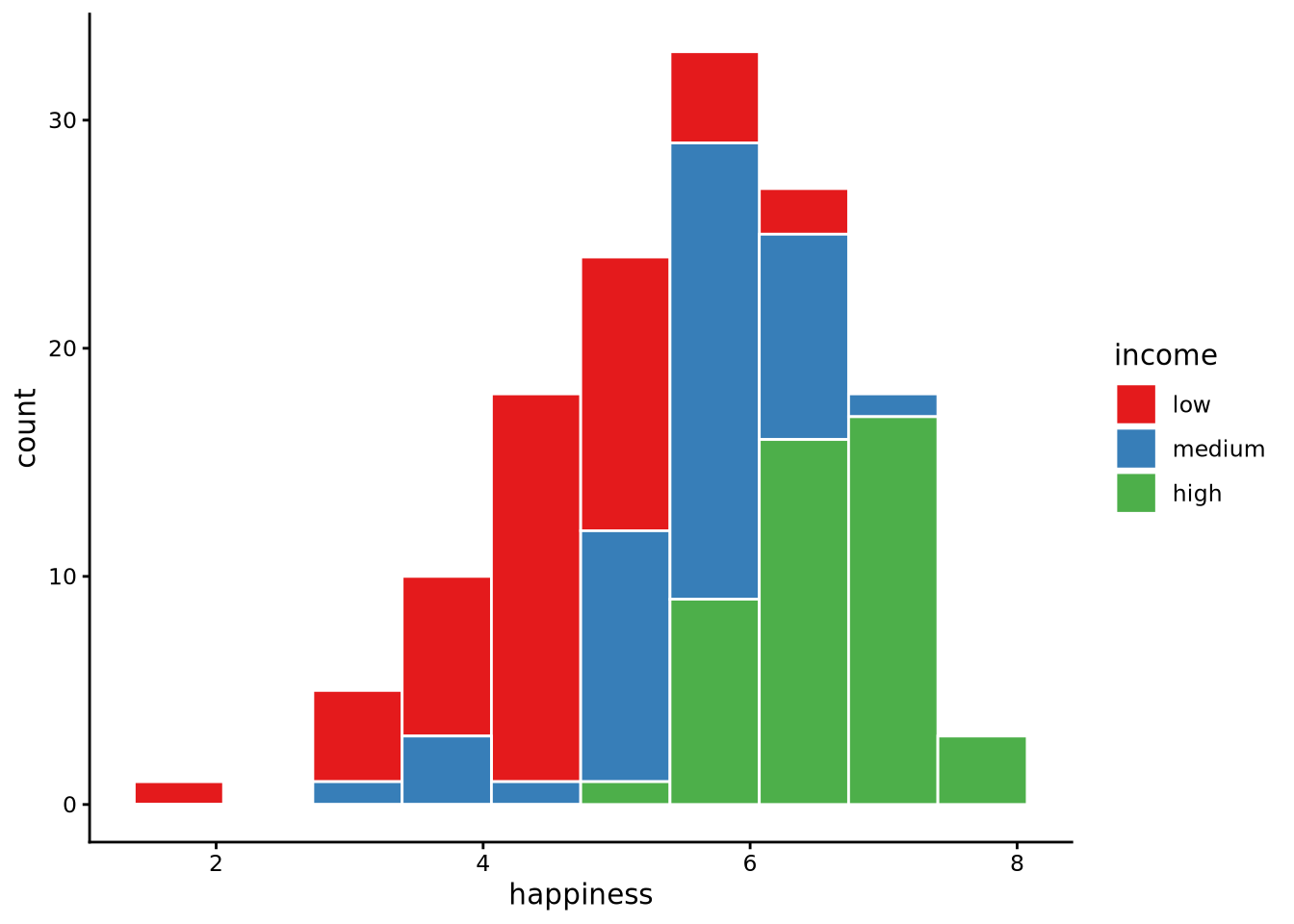
In general, a stacked histogram breaks one numeric variable into bins as usual but fills each bar with coloured segments that represent levels of a second (categorical) variable. In the code above, the bins are along the happiness axis as before, but inside every bin the counts for income = low, medium, and high are stacked vertically. The total height of a bar shows how many countries fall in each bin, while the coloured slices reveal the mix of income tiers within that interval. With a stacked histogram, we can see how many observations are within each bin by the height of the bar, and we can see the proportion of the observations in each bin that are from each income band. For example, for high happiness scores, most or all observations are from the high income countries; for the low happiness scores, most or all observations are from the low income countries.
An alternative conditional histogram approach is to use a dodged histogram as follows:
histogram(happiness, by = income, data = whr2025, position = 'dodge')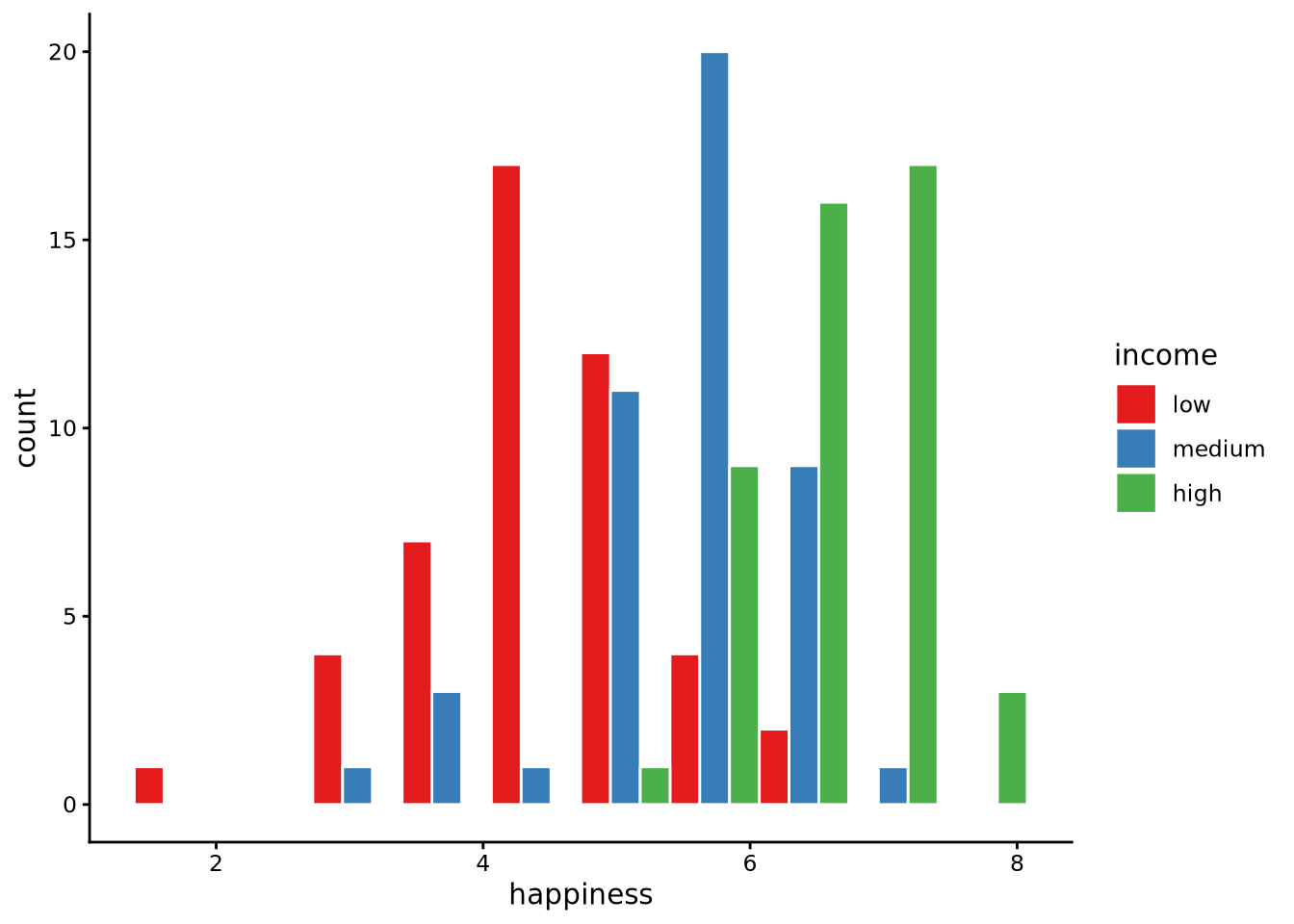
With position = "dodge" the bars belonging to the different income groups are placed side by side instead of on top of one another. Each bin along the happiness axis still has the same overall width, but inside that bin you now see three adjacent bars: one for low-, one for medium-, and one for high-income countries. This layout makes it easy to compare the absolute counts for each income tier at the same happiness level, because the bars share the same baseline. What you give up is a direct sense of the total frequency in each bin: the eye now has to add the separate bar heights rather than reading a single combined column.
Another approach is to produce an identity histogram with position = "identity".
histogram(happiness, by = income, data = whr2025, position = 'identity', alpha = 0.6)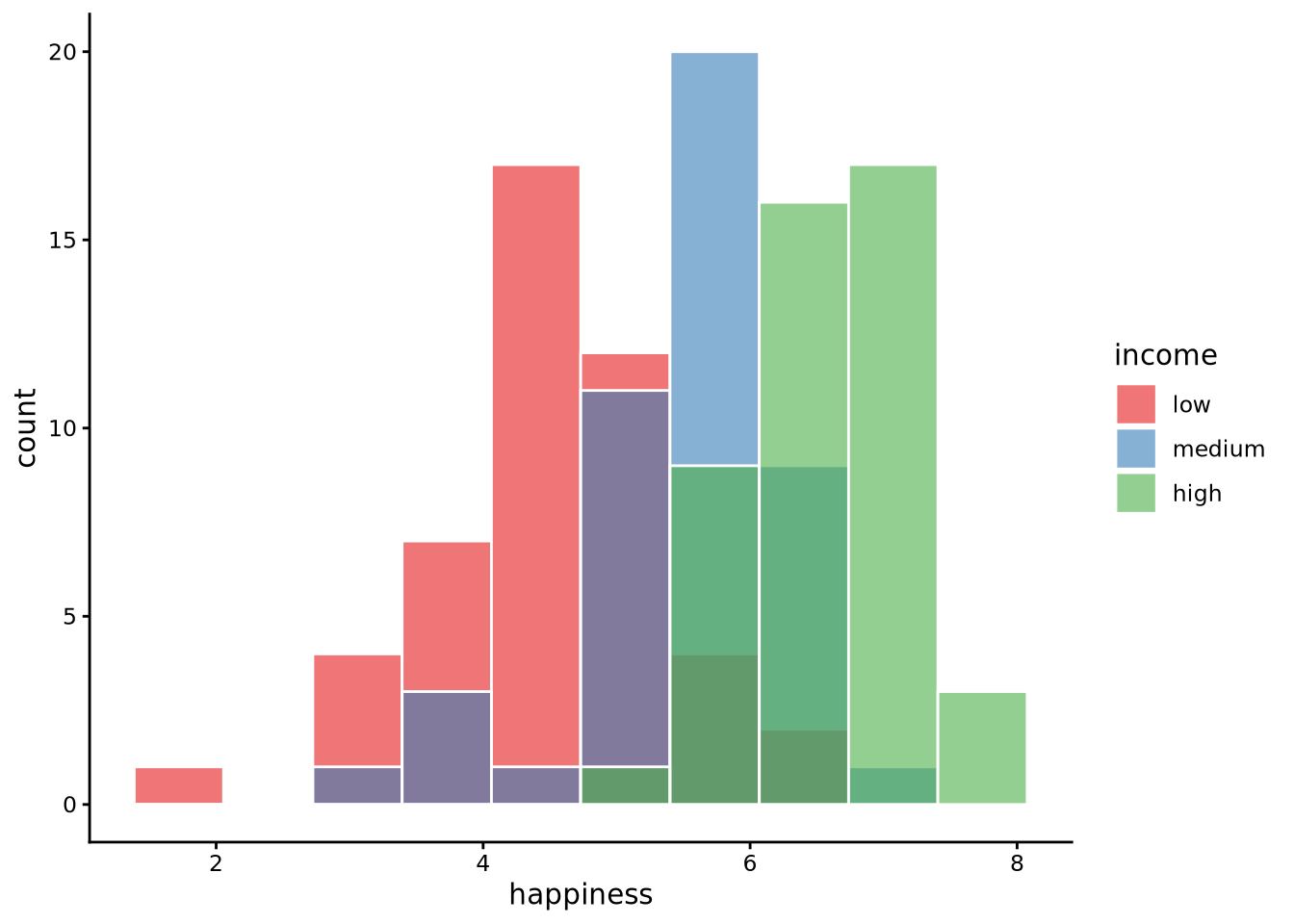
In this case, the bars for the three income groups are drawn directly on top of one another, sharing the same x-coordinates. Setting alpha = 0.6 makes the bars partially transparent so that overlaps are visible. The result resembles three separate histograms superimposed: you can trace the full shape of each income tier’s happiness distribution on a common axis, see where one group dominates or overlaps another, and still read approximate frequencies from the bar heights. Because the bars overlap, however, exact counts for any one bin must be inferred from the colour layering rather than a clean bar outline. Even with partial transparency, however, overlapping bars can obscure one another, so it is not always easy to see the precise shape of each subgroup’s distribution. The identity overlay excels at showing where groups coincide or diverge, but if you need exact bin counts per subgroup a dodged or stacked display is usually clearer.
A final approach is to produce a separate subplot for each subgroup as follows:
histogram(happiness, data = whr2025) + facet_wrap(~income)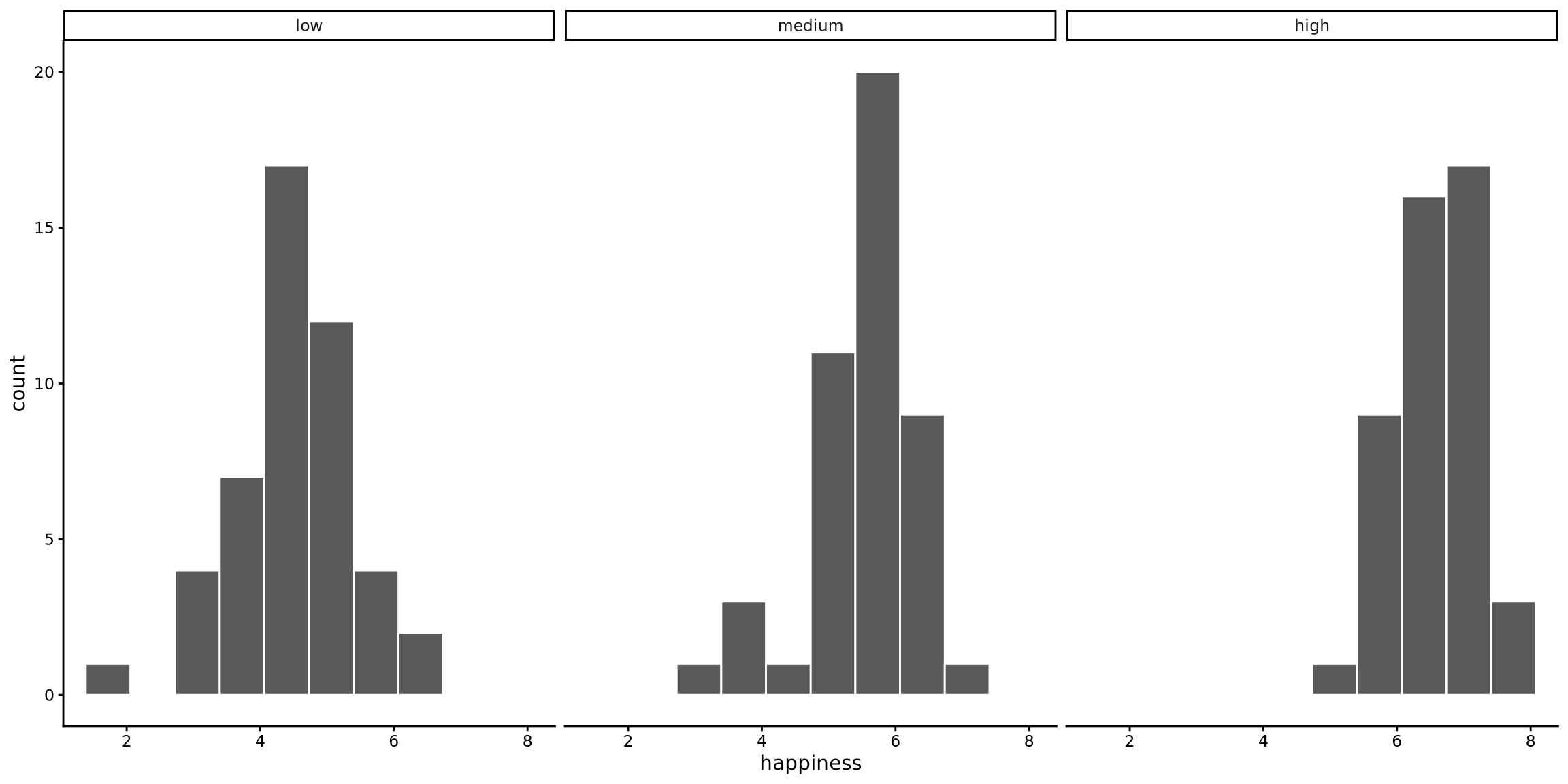
Here, we are using the facet_wrap() function from ggplot2, which will be loaded if tidyverse is loaded. With facet_wrap(~ income) the command draws one histogram panel for each income tier. All three panels share identical bin breaks and axis scales. This small-multiples layout separates the groups completely so their bars never overlap. You can compare shapes — centre, spread, tails — by scanning across aligned panels. Bar heights give exact counts for each subgroup without any need to disentangle stacked or dodged bars. What you lose is a single picture of the overall distribution, but faceting is the clearest way to examine each subgroup in isolation.
3.6.2 Conditional descriptive statistics
All these uses of summarise() for calculating descriptive statistics can be easily extended to perform conditional or grouped descriptive statistics by simply using .by = ....
The code below, for example, calculates the mean, median, standard deviation, and median absolute deviation of happiness separately for each income group:
summarise(
whr2025,
mean_happiness = mean(happiness),
median_happiness = median(happiness),
sd_happiness = sd(happiness),
mad_happiness = mad(happiness),
.by = income # group by the income factor
)# A tibble: 3 × 5
income mean_happiness median_happiness sd_happiness mad_happiness
<ord> <dbl> <dbl> <dbl> <dbl>
1 low 4.51 4.47 0.890 0.818
2 medium 5.55 5.72 0.801 0.655
3 high 6.62 6.66 0.529 0.562income has the ordered levels low < medium < high, so the output shows a tidy table of descriptive statistics, one row per income tercile. We see that as income increases so too do the mean and median average life satisfaction. We see some change in dispersion too. Higher income countries have slightly less variability in their average life satisfaction scores than the lower income countries.
In general, you supply a variable name to .by and summarise() temporarily splits the data into all unique combinations of this variable. For each group, it evaluates every summary function you write. The result is a tibble that contains the .by columns followed by your summary columns. You can, in fact, group by more than one variable at the same time. For example, assuming we had a variable region, we could do .by = c(region, income) to get summaries for every combination of region and income group.
3.6.3 Scatterplots and correlations
Conditional distributions are only possible if the second variable has a small number of distinct values and there are many observations per value. By contrast, when the second variable is continuous — for example, gdp — there are a large number of distinct values and only one or two observations for each value. In this case, conditional boxplots, histograms, and conditional summary statistics are either impossible to calculate or are practically meaningless. In cases like these, we can easily plot each pair of happiness and gdp values as points whose horizontal coordinate is one variable and vertical coordinate is the other. The resulting cloud of dots is called a scatterplot. In the following code, we use the scatterplot() function in sgsur to produce a scatterplot of happiness and gdp:
scatterplot(x = gdp, y = happiness, data = whr2025)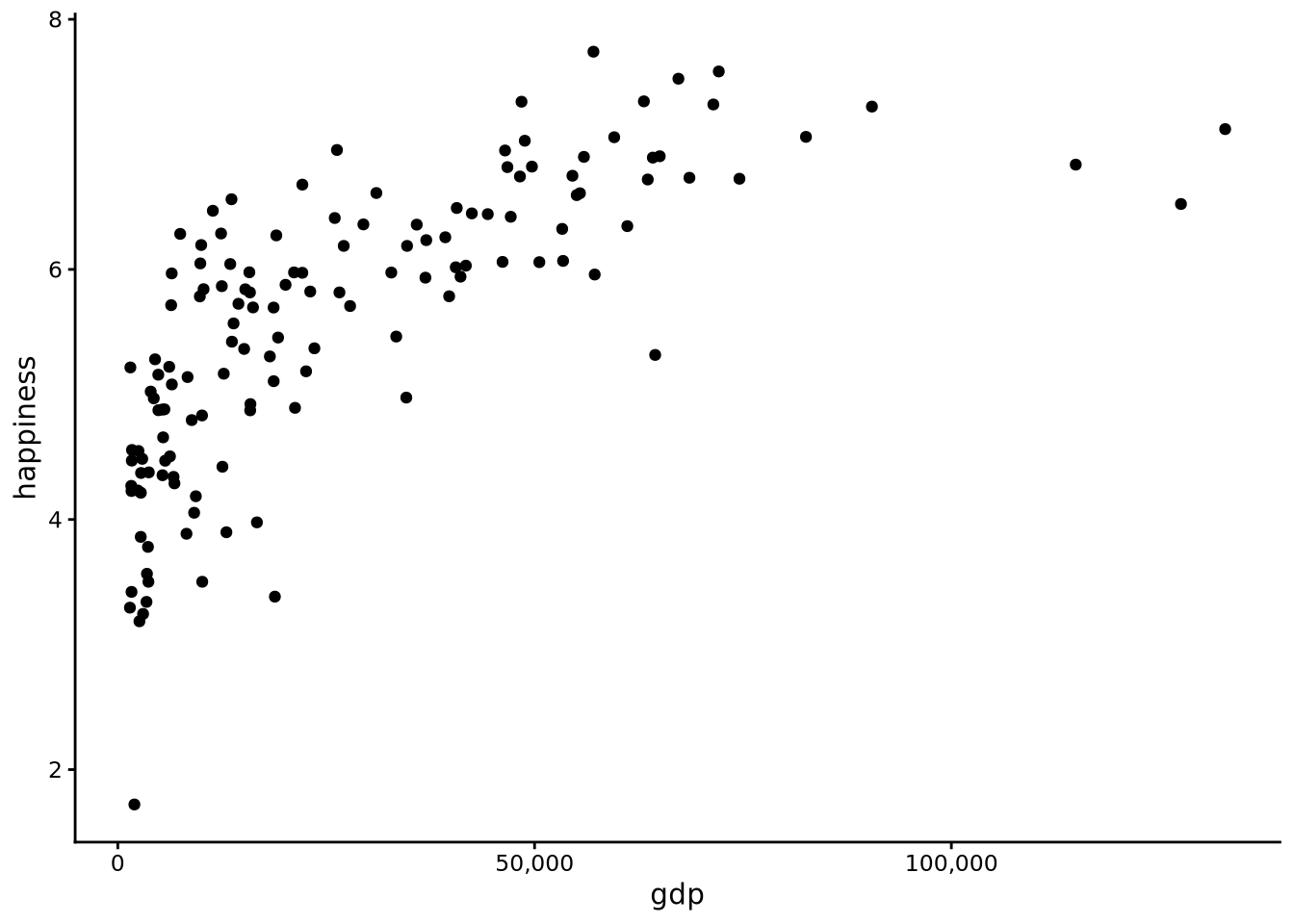
Here we see that as gdp rises from very low to moderate levels, average life satisfaction increases sharply, but the gain tapers off among the wealthiest nations. In other words, there is a positive relationship, though not exactly linear, between gdp and happiness: as one rises, the other rises too, but this relationship is not exactly like a straight line.
To enhance the scatterplot visualisation, we can add a smoother line. Think of this line as a flexible “trend-finder.” It slides a small window along the x-axis, fitting a straight line to just the points in that neighbourhood and giving closer points more weight. As the window moves, those individual local fits are stitched together into one smooth curve, so you see the overall pattern in the cloud of dots without assuming any particular functional relationship, such as a straight line, in advance. We can do this by adding + geom_smooth() after the scatterplot function call:
scatterplot(x = gdp, y = happiness, data = whr2025) + geom_smooth()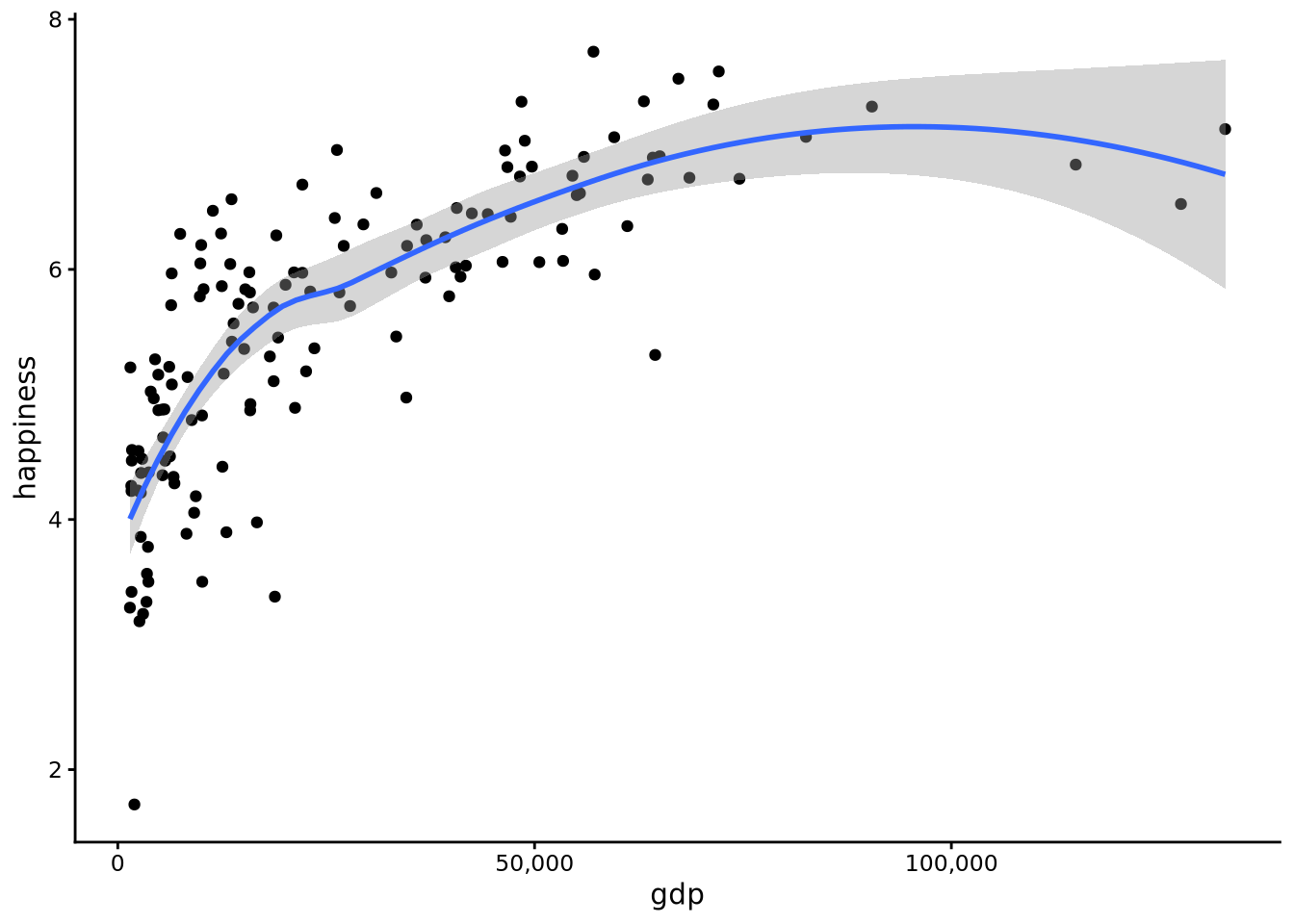
This smoother reveals a rising but nonlinear relationship: happiness increases rapidly as GDP rises from very low levels, but the rate of increase slows considerably as countries become wealthier, with the curve flattening out among the richest nations.
Once we see a relationship, we usually want a number that summarises how strong that pattern is. That job is done by a correlation coefficient. There are different kinds of correlation coefficients, but their values always range from -1 to +1. The sign (positive, negative) of the correlation shows direction: a positive value means the two variables tend to rise together, while a negative value means one tends to rise when the other falls. The size of the correlation, ignoring the sign, shows strength: values close to -1 or +1 indicate a very tight, predictable relationship, whereas values near zero signal a weak or non-existent pattern. Here is a common rule-of-thumb scale for interpreting the absolute value of the coefficient (ignoring the sign):
- 0.00 – 0.09: negligible / trivial
- 0.10 – 0.29: small / weak
- 0.30 – 0.49: moderate / medium
- 0.50 – 0.69: large / strong
- 0.70 – 0.89: very strong
- 0.90 – 1.00: nearly perfect
Different research areas adjust these cut-offs to suit their data and research objectives, so treat the numbers as flexible or approximate guidelines rather than fixed rules.
Two of the most widely used correlation coefficients are Pearson’s and Spearman’s correlations.
Pearson correlation measures the strength and direction of a straight-line relationship between two variables. Suppose the variables are \(x\) and \(y\). Pearson’s correlation coefficient, \(r\), is defined as
\[ r = \frac{\operatorname{cov}(x,y)}{s_x\,s_y}, \]
This is just saying:
- First, calculate the covariance between \(x\) and \(y\).
- Covariance is a measure of how two variables vary together.
- A positive value means that when \(x\) is above its mean, \(y\) also tends to be above its mean.
- A negative value means the opposite — when \(x\) is above its mean, \(y\) tends to be below its mean.
- Then, divide this covariance by the product (multiplication) of the standard deviations of \(x\) and \(y\) (\(s_x\) and \(s_y\)).
- This step rescales the result so that \(r\) always falls between -1 and +1, no matter the units of \(x\) and \(y\).
The result is a clean, unit-free number that captures both the direction (positive or negative) and the strength (closer to 0 = weak, closer to ±1 = strong) of the straight-line relationship.
Spearman correlation is a close cousin. It first converts both variables to ranks (1st, 2nd, 3rd, …) and then applies the same Pearson formula to those ranks instead of the raw values. Because it works with ranks, Spearman picks up any monotonic relationship — one that consistently increases or decreases — not just straight lines. It also makes Spearman less sensitive to extreme outliers, which can pull Pearson’s \(r\) around.
We can use the cor() function built in to R inside the summarise() function to calculate correlations. By default, cor() calculates the Pearson correlation, and so we use method = 'spearman' to obtain Spearman’s correlation.
summarise(
whr2025,
pearson_cor = cor(gdp, happiness),
spearman_cor = cor(gdp, happiness, method = "spearman")
)# A tibble: 1 × 2
pearson_cor spearman_cor
<dbl> <dbl>
1 0.713 0.830The Pearson coefficients tell us how tightly the scatterplot hugs a straight line. By contrast, Spearman’s coefficient tells how tightly the scatterplot adheres to a monotonic function (one that rises consistently or falls consistently, but not necessarily in a straight line). Both coefficients are high — both very strong according to the rules of thumb presented above — but Spearman’s is higher due to the fact that the relationship between gdp and happiness is rising but not in a straight line (nonlinear).
3.7 Further Reading and Watching
For extra background on exploratory data analysis and descriptive statistics, these resources are especially useful:
Exploratory Data Analysis by John W. Tukey (1977). The original source — timeless in philosophy. Great for seeing where the “look before you test” idea comes from.
Fundamentals of Data Visualization by Claus Wilke (2019). Free online at clauswilke.com/dataviz. Excellent for building intuition on what different plots actually show (and don’t show).
Kurtosis as Peakedness, 1905–2014: R.I.P. by Paul H. Westfall (2014). A neat historical paper in The American Statistician that clears up common misconceptions about kurtosis.
StatQuest with Josh Starmer (YouTube). Clear, visual explanations with just the right level of humour. Especially recommended: his videos on variance, standard deviation, skewness, and correlation.
3.8 Chapter summary
What you learned - The role of exploratory data analysis (EDA) as the first step in understanding a dataset before formal modelling or inference. - How to inspect datasets with quick checks (print(), glimpse(), skim()), and why codebooks are essential for decoding variables. - The main types of variables in statistics (continuous, categorical, ordinal, count) and how they relate to R’s data types. - How to describe distributions with plots (histograms, Tukey boxplots) and numbers (mean, median, mode, range, IQR, variance, SD, MAD). - How to interpret centre, spread, and shape (symmetry, tails, skewness, kurtosis). - How to compare groups with conditional plots and grouped summary statistics. - How to explore relationships between variables using scatterplots and correlation (Pearson’s for linear, Spearman’s for monotonic).
Common pitfalls to avoid - Confusing R’s storage type with the true statistical type of your data (e.g. treating ordinal scales as continuous just because they are stored as numbers). - Relying only on one summary (like the mean or range) without checking robustness against outliers or skew. - Overloading a histogram with too many or too few bins, obscuring patterns. - Jumping into modelling before you’ve run health checks and looked at the data’s structure.
Takeaway EDA is your “getting-to-know-you” stage with data: you inspect, visualise, and summarise to spot its centre, spread, shape, and relationships. It helps you identify problems, generate hypotheses, and prepare for inference. With these habits, you’re better equipped to judge what your data can and cannot tell you — and to avoid being misled by quirks, outliers, or hidden structure.